Graph the rational function.
Table of contents
- 0. Review of Algebra4h 18m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations1h 43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 5m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 22m
- 10. Combinatorics & Probability1h 45m
5. Rational Functions
Graphing Rational Functions
Problem 63
Textbook Question
Graph each rational function. ƒ(x)=(x+2)/(x-3)
 Verified step by step guidance
Verified step by step guidance1
Identify the rational function given: \(f(x) = \frac{x+2}{x-3}\).
Determine the vertical asymptote by finding the values of \(x\) that make the denominator zero. Set \(x - 3 = 0\) and solve for \(x\).
Find the horizontal asymptote by comparing the degrees of the numerator and denominator. Since both numerator and denominator are degree 1, the horizontal asymptote is the ratio of the leading coefficients.
Calculate the \(x\)-intercept by setting the numerator equal to zero and solving for \(x\): \(x + 2 = 0\).
Calculate the \(y\)-intercept by evaluating \(f(0)\), which means substituting \(x = 0\) into the function.
 Verified video answer for a similar problem:
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
7mPlay a video:
0 Comments
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Rational Functions
A rational function is a ratio of two polynomials, expressed as f(x) = P(x)/Q(x), where Q(x) ≠ 0. Understanding the form helps identify domain restrictions and behavior, such as vertical asymptotes where the denominator is zero.
Recommended video:

Intro to Rational Functions
Domain and Vertical Asymptotes
The domain of a rational function excludes values that make the denominator zero. These values often correspond to vertical asymptotes, where the function approaches infinity or negative infinity, indicating points of discontinuity on the graph.
Recommended video:
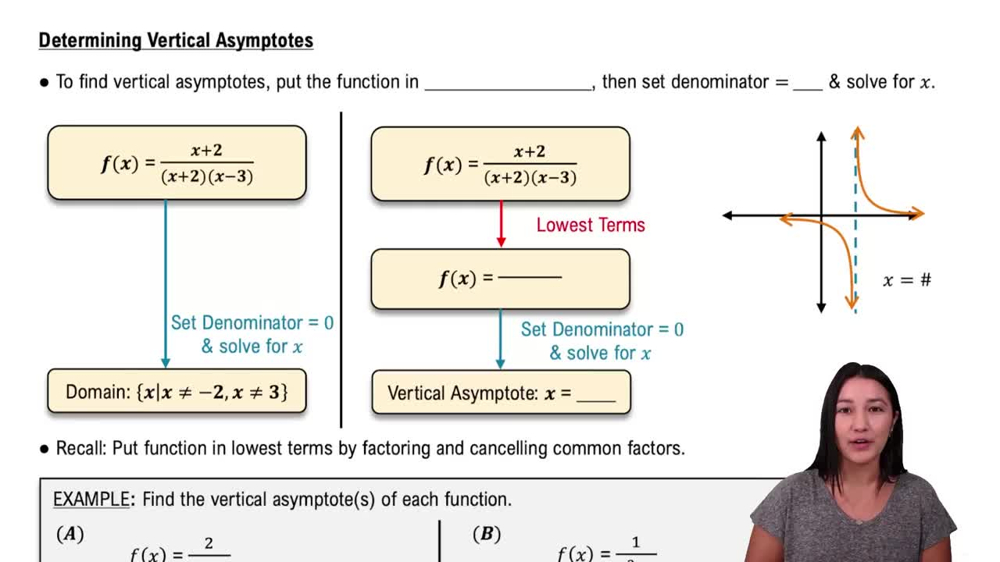
Determining Vertical Asymptotes
Graphing Rational Functions
Graphing involves identifying intercepts, asymptotes (vertical, horizontal, or oblique), and behavior near these lines. For f(x) = (x+2)/(x-3), find zeros, vertical asymptotes at x=3, and horizontal asymptotes by comparing degrees of numerator and denominator.
Recommended video:
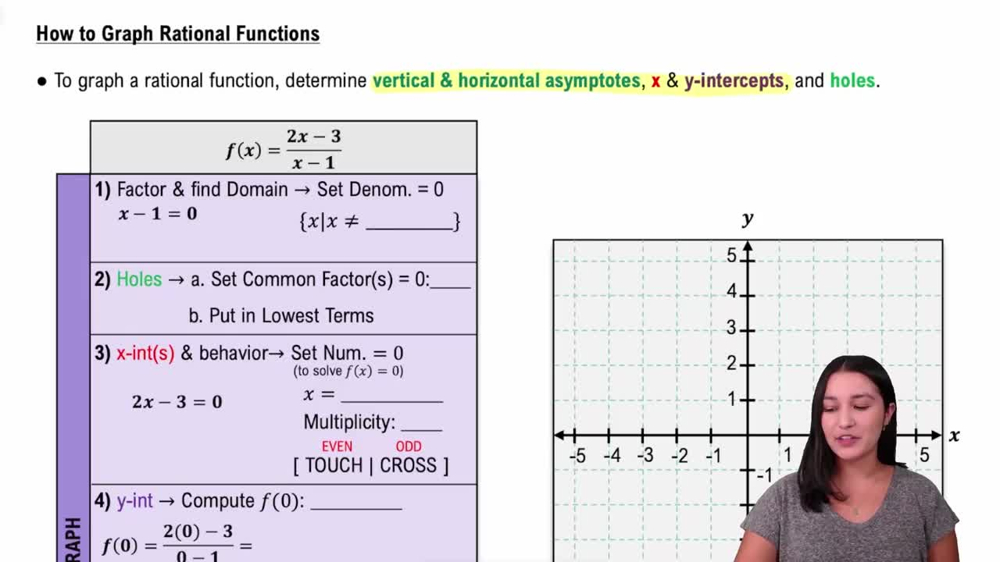
How to Graph Rational Functions
Related Videos
Related Practice
Multiple Choice
1052
views
1
rank


