The graph of a function ƒ is shown in the figure. Sketch the graph of each function defined as follows.

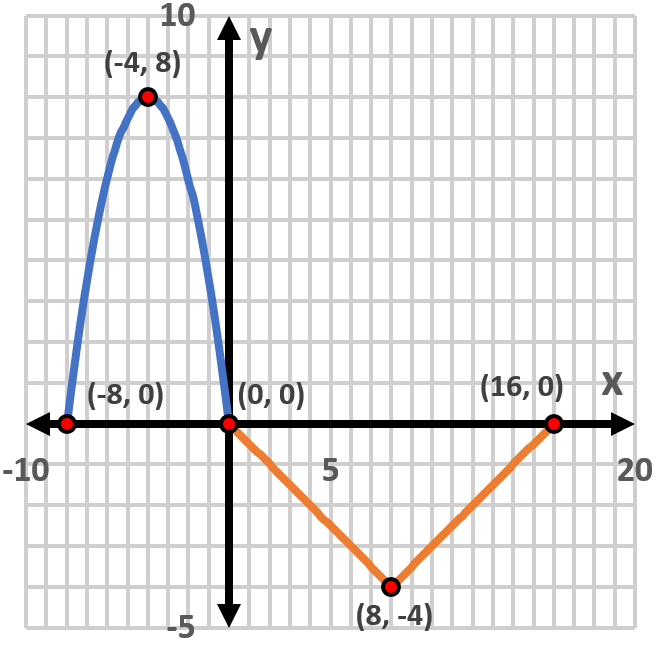
(c) y = ƒ(x+3) - 2

Verified step by step guidance

1. Identify the original function ƒ and its key points from the graph. The points given are (-8, 0), (-4, 8), (0, 0), (8, -4), and (16, 0).
2. Understand the transformation y = ƒ(x + 3) - 2. The term (x + 3) inside the function indicates a horizontal shift to the left by 3 units.
3. The '- 2' outside the function indicates a vertical shift downward by 2 units.
4. Apply the horizontal shift to each x-coordinate of the key points by subtracting 3 (since x is replaced by x + 3, the graph moves left): for example, (-8, 0) becomes (-8 - 3, 0) = (-11, 0).
5. Apply the vertical shift to each y-coordinate by subtracting 2: for example, the point (-11, 0) becomes (-11, 0 - 2) = (-11, -2). Repeat this for all key points to get the new coordinates for the transformed graph.

Key Concepts

Horizontal Shifts of Functions

A horizontal shift involves moving the graph of a function left or right. For y = f(x + c), the graph shifts c units to the left if c is positive, and to the right if c is negative. This transformation changes the input values but not the output values.

Vertical Shifts of Functions

A vertical shift moves the graph of a function up or down without changing its shape. For y = f(x) - k, the graph shifts k units downward if k is positive, and upward if k is negative. This transformation adds or subtracts a constant from the output values.

Combining Transformations

When a function undergoes both horizontal and vertical shifts, each transformation is applied independently. For y = f(x + 3) - 2, first shift the graph 3 units left, then shift it 2 units down. Understanding the order and effect of each shift is essential for accurate graph sketching.