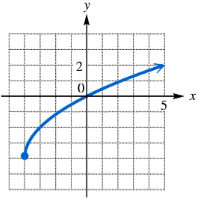
Each of the following graphs is obtained from the graph of ƒ(x)=|x| or g(x)=√x by applying several of the transformations discussed in this section. Describe the transformations and give an equation for the graph.

Verified step by step guidance

1. Step 1: Identify the base function. The graph resembles the shape of the square root function \(g(x) = \sqrt{x}\), but it is shifted and reflected.
2. Step 2: Observe the horizontal shift. The graph starts at \(x = -4\), indicating a shift to the left by 4 units. This suggests the inside of the square root is \((x + 4)\).
3. Step 3: Observe the vertical shift and reflection. The graph is below the x-axis, indicating a reflection across the x-axis (a negative sign in front of the function) and a vertical shift downward. The starting point is at \(y = -4\), so the function is shifted down by 4 units.
4. Step 4: Write the transformed function using the observations: \(y = -\sqrt{x + 4} - 4\).
5. Step 5: Verify the transformations: The graph is the square root function shifted left 4 units, reflected over the x-axis, and shifted down 4 units.

Key Concepts

Square Root Function and Its Graph

The square root function, g(x) = √x, produces a curve starting at the origin (0,0) and increasing slowly to the right. It is defined only for x ≥ 0, and its graph is a half-parabola lying in the first quadrant. Understanding this base graph is essential for identifying transformations.

Transformations of Functions

Transformations include shifts, reflections, stretches, and compressions applied to the base graph. Horizontal shifts move the graph left or right, vertical shifts move it up or down, reflections flip it across axes, and stretches/compressions change its steepness. These changes alter the equation accordingly.

Interpreting Graph Shifts and Reflections

A graph shifted left by h units and down by k units corresponds to g(x + h) - k. A reflection across the x-axis changes the sign of the function, resulting in -g(x). Recognizing these shifts and reflections from the graph helps write the transformed function's equation.