In Exercises 109–114, find the x-intercept(s) of the graph of each equation. Use the x-intercepts to match the equation with its graph. The graphs are shown in [- 10, 10, 1] by [- 10, 10, 1] viewing rectangles and labeled (a) through (f). y = x² - 4x - 5

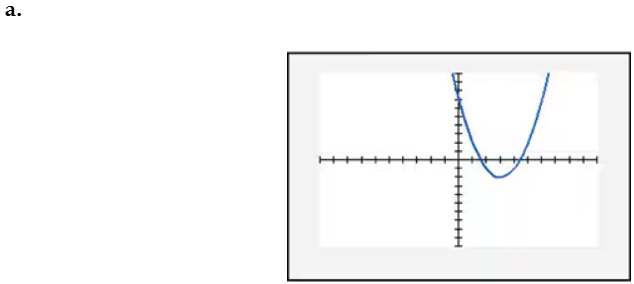
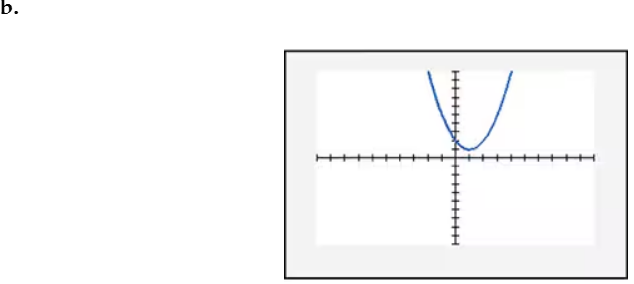
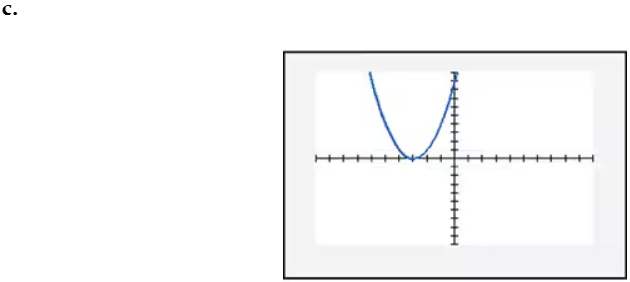
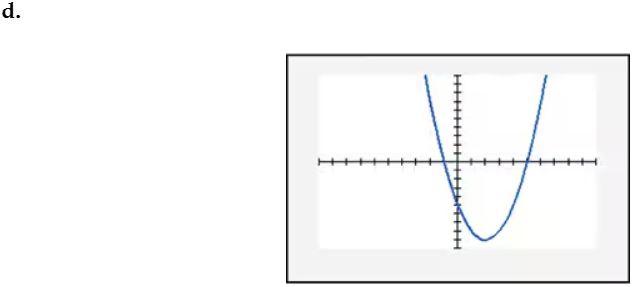
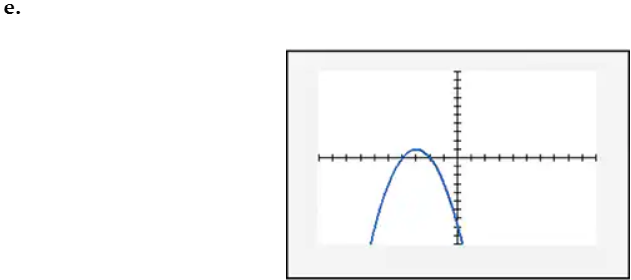
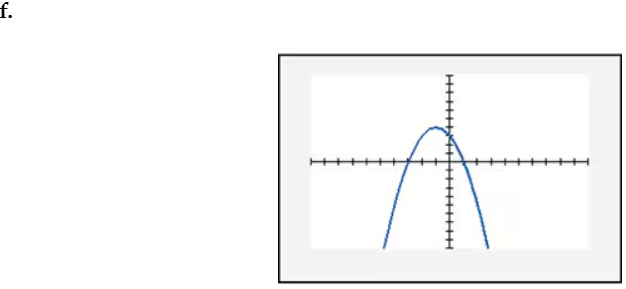
Verified step by step guidance

1. To find the x-intercepts of the graph of the equation y = x^2 - 4x - 5, set y = 0 because the x-intercepts occur where the graph crosses the x-axis (i.e., where y = 0). This gives the equation 0 = x^2 - 4x - 5.
2. Rewrite the equation as x^2 - 4x - 5 = 0. This is a quadratic equation, and we will solve it using factoring, the quadratic formula, or completing the square. In this case, factoring is a good approach.
3. Factor the quadratic equation x^2 - 4x - 5. Look for two numbers that multiply to -5 (the constant term) and add to -4 (the coefficient of x). These numbers are -5 and 1, so the equation factors as (x - 5)(x + 1) = 0.
4. Apply the Zero Product Property, which states that if a product of two factors equals zero, then at least one of the factors must be zero. Set each factor equal to zero: x - 5 = 0 and x + 1 = 0.
5. Solve each equation for x. For x - 5 = 0, add 5 to both sides to get x = 5. For x + 1 = 0, subtract 1 from both sides to get x = -1. Therefore, the x-intercepts are x = 5 and x = -1.

Key Concepts

X-Intercept

The x-intercept of a graph is the point where the graph intersects the x-axis. This occurs when the value of y is zero. To find the x-intercept(s) of an equation, you set y equal to zero and solve for x. In the context of the given equation, this means solving the quadratic equation x^2 - 4x - 5 = 0.

Quadratic Equations

A quadratic equation is a polynomial equation of the form ax^2 + bx + c = 0, where a, b, and c are constants, and a is not zero. The solutions to a quadratic equation can be found using factoring, completing the square, or the quadratic formula. Understanding how to manipulate and solve these equations is essential for finding x-intercepts.

Graphing Quadratics

Graphing a quadratic function involves plotting a parabolic curve that opens upwards or downwards, depending on the sign of the leading coefficient (a). The vertex of the parabola represents the maximum or minimum point, while the x-intercepts indicate where the graph crosses the x-axis. Recognizing the shape and key features of quadratic graphs is crucial for matching equations to their corresponding graphs.