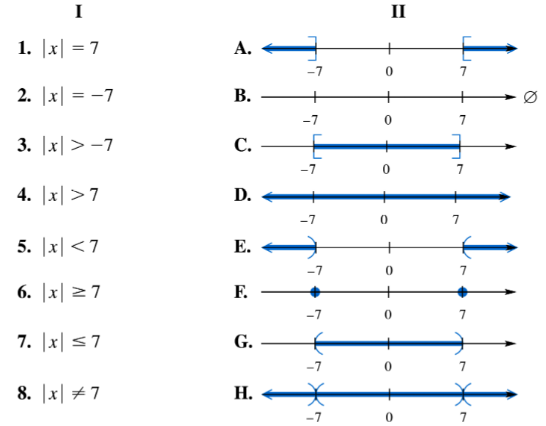
Match each equation or inequality in Column I with the graph of its solution set in Column II. | x | = 7

Verified step by step guidance

Understand the equation given: \(|x| = 7\). This means the absolute value of \(x\) is equal to 7.

Recall that the absolute value \(|x|\) represents the distance of \(x\) from 0 on the number line, regardless of direction.

Set up two equations based on the definition of absolute value: \(x = 7\) and \(x = -7\).

Recognize that the solution set consists of two points on the number line: one at 7 and one at -7.

Match this solution set to the graph in Column II that shows exactly these two points, and no other values.

Verified video answer for a similar problem:

This video solution was recommended by our tutors as helpful for the problem above.

Video duration:

Was this helpful?

Key Concepts

Here are the essential concepts you must grasp in order to answer the question correctly.

Absolute Value Definition

The absolute value of a number represents its distance from zero on the number line, always as a non-negative value. For example, |x| = 7 means x is 7 units away from zero, so x can be either 7 or -7.

Solving Absolute Value Equations

To solve an equation like |x| = a, where a > 0, split it into two cases: x = a and x = -a. This reflects the two points on the number line that satisfy the distance condition.

Graphing Solution Sets on the Number Line

The solution set of |x| = 7 consists of two points, x = 7 and x = -7. On a graph, these are represented as two distinct points on the number line, showing all values that satisfy the equation.