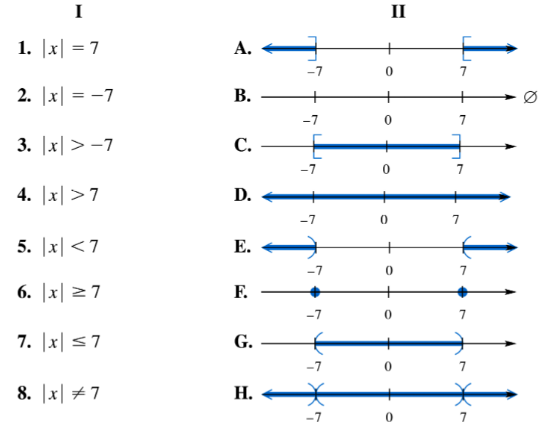
Match each equation or inequality in Column I with the graph of its solution set in Column II. | x | = -7

Verified step by step guidance

1. Recognize that the equation involves the absolute value function: \(|x| = -7\).
2. Recall the definition of absolute value: for any real number \(x\), \(|x|\) represents the distance of \(x\) from zero on the number line, which is always non-negative.
3. Since absolute value cannot be negative, the equation \(|x| = -7\) has no real solutions.
4. Understand that the graph of the solution set will be the empty set, meaning no points on the number line satisfy this equation.
5. Therefore, when matching to graphs, look for the graph that shows no solution or an empty set.

Key Concepts

Absolute Value Definition

The absolute value of a number represents its distance from zero on the number line and is always non-negative. For any real number x, |x| ≥ 0, meaning absolute value cannot be negative.

Solving Absolute Value Equations

When solving equations involving absolute values, such as |x| = a, the value a must be non-negative. If a is negative, like |x| = -7, there is no solution because absolute values cannot equal negative numbers.

Graphing Solution Sets of Equations

Graphs of solution sets represent all values satisfying the equation or inequality. For equations with no solution, like |x| = -7, the graph will show an empty set or no points, indicating no values satisfy the condition.