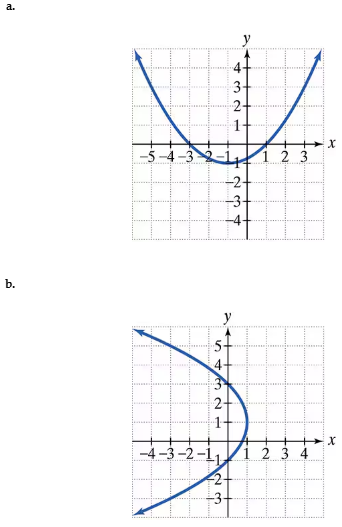
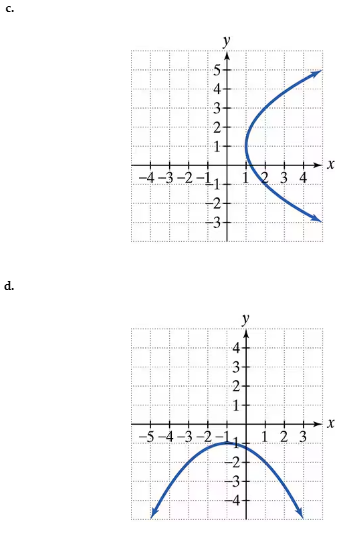
In Exercises 31–34, find the vertex, focus, and directrix of each parabola with the given equation. Then match each equation to one of the graphs that are shown and labeled (a)–(d). (y - 1)² = - 4(x - 1)

Verified step by step guidance

1. Identify the form of the given equation. The equation is \((y - 1)^2 = -4(x - 1)\), which matches the standard form of a horizontally oriented parabola: \((y - k)^2 = 4p(x - h)\), where \((h, k)\) is the vertex and \(p\) determines the distance and direction of the focus and directrix.
2. From the equation, extract the vertex \((h, k)\). Here, \(h = 1\) and \(k = 1\), so the vertex is \((1, 1)\).
3. Identify the value of \(4p\) from the equation. We have \(4p = -4\), so \(p = -1\). The negative sign indicates the parabola opens to the left (since it is horizontal and \(p < 0\)).
4. Find the focus using the vertex and \(p\). For a horizontal parabola, the focus is at \((h + p, k)\). Substitute \(h = 1\), \(k = 1\), and \(p = -1\) to get the focus at \((1 - 1, 1) = (0, 1)\).
5. Find the directrix, which is a vertical line given by \(x = h - p\). Substitute \(h = 1\) and \(p = -1\) to get the directrix as \(x = 1 - (-1) = 2\).

Key Concepts

Standard Form of a Parabola

The standard form of a parabola's equation helps identify its orientation and key features. For parabolas that open left or right, the form is (y - k)^2 = 4p(x - h), where (h, k) is the vertex and p determines the distance to the focus and directrix. Recognizing this form allows you to extract important information directly from the equation.

Vertex, Focus, and Directrix of a Parabola

The vertex is the parabola's turning point, given by (h, k). The focus lies inside the parabola, at a distance p from the vertex along the axis of symmetry. The directrix is a line perpendicular to the axis of symmetry, located p units opposite the focus. These elements define the parabola's shape and position.

Graph Matching Using Parabola Features

Matching an equation to a graph involves using the vertex, focus, and directrix to identify the parabola's orientation and position. By calculating these features from the equation, you can compare them to the labeled graphs and select the correct match based on shape and location.