Solve each equation. 4x-2 = 23x+3
Table of contents
- 0. Review of Algebra4h 18m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations1h 43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 5m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 22m
- 10. Combinatorics & Probability1h 45m
6. Exponential & Logarithmic Functions
Introduction to Exponential Functions
Problem 1
Textbook Question
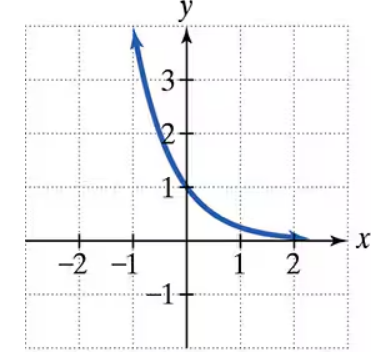
The graph of an exponential function is given. Select the function for each graph from the following options: f(x) = 4x, g(x) = 4-x, h(x) = -4-x, r(x) = -4-x+3
 Verified step by step guidance
Verified step by step guidance1
Step 1: Identify the point given on the graph, which is (0, 2). This point represents the y-intercept of the function, so when x = 0, y = 2.
Step 2: Evaluate each function option at x = 0 to see which one gives y = 2. Recall that for any base a, a^0 = 1.
Step 3: Calculate f(0) = 4^0 = 1, g(0) = 4^{-0} = 4^0 = 1, h(0) = -4^{-0} = -1, and r(0) = -4^{-0} + 3 = -1 + 3 = 2.
Step 4: Since only r(0) equals 2, the function must be r(x) = -4^{-x} + 3.
Step 5: Confirm the shape of the graph matches the function r(x) = -4^{-x} + 3, which is a reflection and vertical shift of the exponential decay function.
 Verified video answer for a similar problem:
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
4mPlay a video:
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Exponential Functions and Their Graphs
An exponential function has the form f(x) = a^x, where a > 0 and a ≠ 1. Its graph shows rapid growth if a > 1 and decay if 0 < a < 1. The y-intercept is always at (0,1) for f(x) = a^x, since any number to the zero power is 1, unless the function is transformed.
Recommended video:

Graphs of Exponential Functions
Transformations of Exponential Functions
Transformations include reflections, shifts, and stretches. For example, f(x) = 4^-x reflects the graph of 4^x across the y-axis, changing growth to decay. Adding or subtracting constants shifts the graph vertically, affecting the y-intercept and horizontal asymptotes.
Recommended video:

Transformations of Exponential Graphs
Using Points to Identify Functions
Given a point on the graph, such as (0,2), substitute x = 0 into each function to find the corresponding y-value. This helps determine which function matches the graph. For instance, f(0) = a^0 = 1, so if y ≠ 1 at x=0, the function must include vertical shifts or reflections.
Recommended video:

Maximum Turning Points of a Polynomial Function

 6:13m
6:13mWatch next
Master Exponential Functions with a bite sized video explanation from Patrick
Start learningRelated Videos
Related Practice
Textbook Question
599
views
