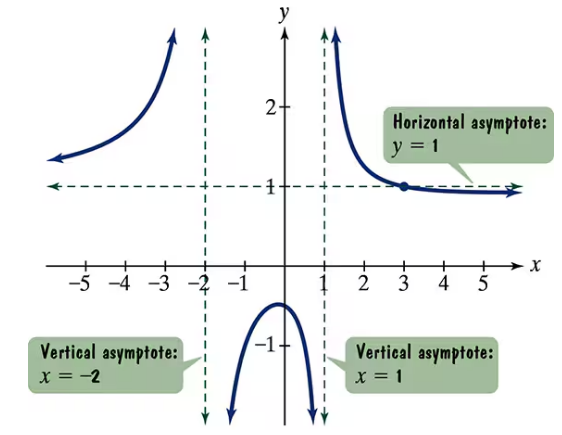
Use the graph of the rational function in the figure shown to complete each statement in Exercises 15–20.

As $x \to - 2^{+}, f (x) \to$ __

Verified step by step guidance

Identify the vertical asymptote relevant to the limit as $x \to -2^+$. From the graph, note the vertical asymptotes are at $x = -16$ and $x = -8$, so $x = -2$ is not a vertical asymptote, but we need to observe the behavior of $f(x)$ near $x = -2$ from the right side.

Look closely at the graph near $x = -2$ from the right side (values slightly greater than -2). Observe the value of $f(x)$ as $x$ approaches -2 from the right.

Determine whether $f(x)$ is increasing or decreasing without bound, or approaching a finite value as $x \to -2^+$. This will tell us if the function tends to $+\infty$, $-\infty$, or a finite number.

Based on the graph, note the trend of the function near $x = -2^+$. If the function approaches a horizontal asymptote or a specific value, that will be the limit.

Conclude the value of $\lim_{x \to -2^+} f(x)$ by describing the behavior observed in the previous steps.

Verified video answer for a similar problem:

This video solution was recommended by our tutors as helpful for the problem above.

Video duration:

Was this helpful?

Key Concepts

Here are the essential concepts you must grasp in order to answer the question correctly.

Vertical Asymptotes

Vertical asymptotes occur where the function approaches infinity or negative infinity as x approaches a specific value. These are typically values that make the denominator of a rational function zero, causing the function to be undefined. The graph shows vertical asymptotes at x = -16 and y = 17, indicating behavior near these lines.

Horizontal Asymptotes

Horizontal asymptotes describe the behavior of a function as x approaches positive or negative infinity. They represent a constant value that the function approaches but does not necessarily reach. In the graph, the horizontal asymptote is at x = -8, which is unusual since horizontal asymptotes are usually horizontal lines y = c, suggesting a possible labeling or interpretation detail.

Limit Behavior Near Asymptotes

Understanding the limit of a function as x approaches a value from the left or right is crucial for analyzing asymptotic behavior. For example, as x approaches -2 from the right (x → -2^+), the function's value may approach positive or negative infinity or a finite number. This concept helps predict the function's behavior near discontinuities or asymptotes.

Recommended video:

6:24

Introduction to Asymptotes

Related Practice

Textbook Question

In Exercises 15–18, use the Leading Coefficient Test to determine the end behavior of the graph of the given polynomial function. Then use this end behavior to match the polynomial function with its graph. [The graphs are labeled (a) through (d).] <IMAGE>

$f (x) = (x - 3)^{2}$

605

views

Textbook Question

Use the vertex and intercepts to sketch the graph of each quadratic function. Give the equation of the parabola's axis of symmetry. Use the graph to determine the function's domain and range. f(x)=(x−4)²−1

1309

views

Textbook Question

In Exercises 17–24, a) List all possible rational roots. b) List all possible rational roots. c) Use the quotient from part (b) to find the remaining roots and solve the equation. x³−2x²−11x+12=0

561

views

Textbook Question

Find the zeros for each polynomial function and give the multiplicity of each zero. State whether the graph crosses the x-axis, or touches the x-axis and turns around, at each zero. $f (x) = - 2 (x - 1) (x + 2)^{2} (x + 5)^{3}$