Find the domain of the rational function. Then, write it in lowest terms.
Table of contents
- 0. Review of Algebra4h 18m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations1h 43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 5m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 22m
- 10. Combinatorics & Probability1h 45m
5. Rational Functions
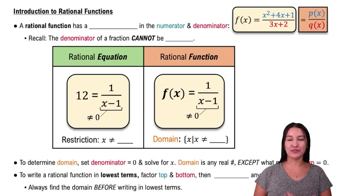
Introduction to Rational Functions
Problem 7
Textbook Question
Find the domain of each rational function. f(x)=(x+7)/(x2+49)
 Verified step by step guidance
Verified step by step guidance1
Identify the rational function given: \(f(x) = \frac{x+7}{x^{2} + 49}\).
Recall that the domain of a rational function includes all real numbers except where the denominator is zero, because division by zero is undefined.
Set the denominator equal to zero to find values to exclude: \(x^{2} + 49 = 0\).
Solve the equation \(x^{2} + 49 = 0\) by isolating \(x^{2}\): \(x^{2} = -49\).
Since \(x^{2} = -49\) has no real solutions (because a square cannot be negative in the real number system), the denominator is never zero for any real \(x\), so the domain is all real numbers.
 Verified video answer for a similar problem:
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
1mPlay a video:
0 Comments
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Domain of a Function
The domain of a function is the set of all possible input values (x-values) for which the function is defined. For rational functions, the domain excludes any x-values that make the denominator zero, as division by zero is undefined.
Recommended video:

Domain Restrictions of Composed Functions
Rational Functions
A rational function is a ratio of two polynomials, expressed as f(x) = P(x)/Q(x). Understanding the behavior of the numerator and denominator polynomials is essential, especially identifying values that cause the denominator to be zero.
Recommended video:
Intro to Rational Functions
Solving Quadratic Equations
To find values that make the denominator zero, you solve the quadratic equation Q(x) = 0. Techniques include factoring, completing the square, or using the quadratic formula to determine if real roots exist that restrict the domain.
Recommended video:

Solving Quadratic Equations by Factoring

 6:4m
6:4mWatch next
Master Intro to Rational Functions with a bite sized video explanation from Patrick
Start learningRelated Videos
Related Practice
Multiple Choice
724
views
1
rank
1
comments
