Use the graphs of the rational functions in choices A–D to answer each question.

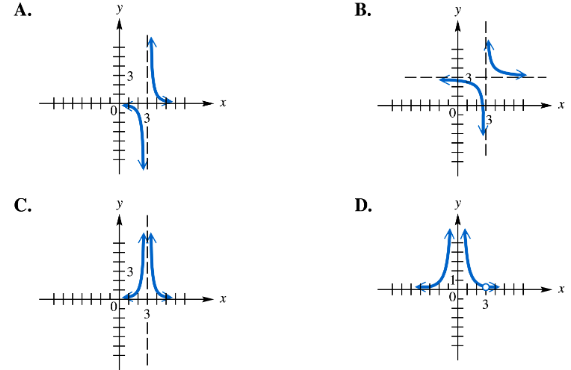
There may be more than one correct choice. If ƒ represents the function, only one choice has a single solution to the equation ƒ(x)=3. Which one is it?

Verified step by step guidance

1. Step 1: Understand the problem. We need to find which graph has exactly one solution to the equation \(f(x) = 3\). This means we are looking for the graph where the horizontal line \(y = 3\) intersects the function's graph exactly once.
2. Step 2: Analyze each graph by visualizing or drawing the horizontal line \(y = 3\) and count the number of intersection points with the graph of \(f(x)\).
3. Step 3: For graph A, observe that the curve crosses the line \(y = 3\) exactly once. This suggests one solution for \(f(x) = 3\).
4. Step 4: For graph B, notice that the curve crosses the line \(y = 3\) more than once, indicating multiple solutions to \(f(x) = 3\).
5. Step 5: For graphs C and D, similarly check the number of intersections with \(y = 3\). Both graphs show two or more intersections, meaning multiple solutions. Therefore, only graph A has a single solution to \(f(x) = 3\).

Key Concepts

Rational Functions and Their Graphs

A rational function is a ratio of two polynomials. Its graph can have vertical asymptotes where the denominator is zero and horizontal or oblique asymptotes describing end behavior. Understanding these features helps interpret the shape and behavior of the graph.

Solving Equations Using Graphs

To solve an equation like f(x) = k graphically, find the points where the graph of f(x) intersects the horizontal line y = k. The number of intersection points corresponds to the number of solutions to the equation.

Interpreting Intersection Points for Solution Count

The number of solutions to f(x) = 3 is the count of x-values where the graph crosses y = 3. Identifying graphs with exactly one intersection with y = 3 is key to answering the question about a single solution.