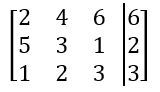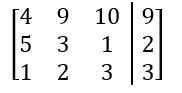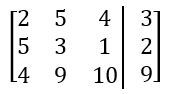In mathematics, a matrix is a structured way to organize numbers into a grid format, consisting of rows and columns. For example, a matrix with 2 rows and 3 columns is referred to as a 2 by 3 matrix. This organization allows for a compact representation of information, particularly useful in systems of equations.
When converting a system of equations into a matrix, the resulting structure is known as an augmented matrix. This matrix includes the coefficients of the variables and the constants from the equations, effectively summarizing the system in a more manageable form. For instance, if you have a system of equations with two equations and three variables, the augmented matrix will reflect this by having two rows and four columns (three for the variables and one for the constants).
To construct an augmented matrix, you extract the coefficients of each variable from the equations. If a variable is absent in an equation, it is represented by a zero in the matrix. For example, consider the equations:
- 2x - 3y + z = -4
- 6x + 3y + 0z = 13
- 0x + y - z = 8
The corresponding augmented matrix would be:
\[\begin{bmatrix}2 & -3 & 1 & | & -4 \\6 & 3 & 0 & | & 13 \\0 & 1 & -1 & | & 8\end{bmatrix}\]
In this matrix, the vertical bar represents the equal sign, separating the coefficients from the constants. This method of representation not only simplifies the visual complexity of systems of equations but also sets the stage for further operations and manipulations that can be performed on matrices, such as addition, subtraction, and finding solutions using techniques like Gaussian elimination.