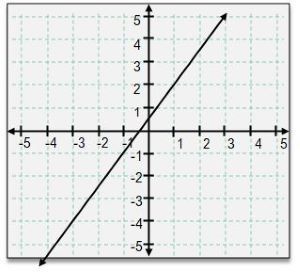
Hey, everyone. So as we've talked about equations with 2 variables, we've seen different shapes of graphs. For example, we've seen perfectly straight lines, but we've also seen things that curve in different ways. Well, for the next few videos, we're only just going to be focusing on lines, and we're going to start our discussion by talking about a very important characteristic of lines, which is called the slope. What I'm going to show you in this video is that the slope is really just a number that you can calculate by using any two points on a line. It's very straightforward. Let me go ahead and take a look. Let's go ahead and take a look here. So the slope is really just a number that represents how steep a line is. So take a look at these two lines and imagine they were like the side of a hill that you're trying to climb. The green one is a little bit more shallow because you don't have to rise as much or go up before you can go over, whereas the red line is a little bit steeper. It's, like, a little bit more vertical. This would be a harder climb. Mathematically, what's going on here is it's how much the y value changes divided by how much the x value changes. So let's take a look at the equation here. The variable that we use for the slope is the variable m, and the equation is y2-y1x2-x1. So I'm going to talk about what those things mean in just a second, but this is a little bit tedious to write out. So we've developed a little bit of a shorthand for this, and we use a little triangle symbol, which is the Greek letter delta. The way that this is written is ΔyΔx just to make it a little bit shorter. And, basically, what the Δy means is it's kind of like the rise of an equation or a graph divided by Δx, which is like the run. Again, think about the steepness here and think about these two lines. Imagine I was trying to get from this point to this point. First on this grass graph, I have to rise a little bit. I have to go up vertically before I can go over. That's what those delta symbols mean here. Alright? So anytime you see this triangle symbol that just means a change in a variable or a difference, And, basically, what's going on here with these y2s and y1s and all that stuff is these are actually just points. So remember that we can locate any point on a graph, which is by an xy pair, But since we have 2 of them, we just give them numbers. And so, really, x2 and y2 are just and x1 and y1 are just 2 points that are on a graph, and they may be given to you, or you might actually have to pick them yourself. Let's go and take a look at an equation or an example so I can show you how this works. We're going to find the slopes of these two lines that we've been seeing in this graph. So, basically, what we have to do is to find the slope of a or this yeah. The slope of a. I just need y2 minus y1 over x2 minus x1. So what are those two points over here? Well, here on the graph, they're actually given to us. We just have to figure out what those ordered pairs are. What are those points x1, y1? So this point over here, I'm going to use this x1, y1, and this is just the point 1, comma, 2. Right? So this is 1, comma, 2. And what's my x2y2? It's just 2 and then 4 in the y. So this is 2, comma, 4. So these are my 2 ordered pairs, and I could basically just plug them into this equation over here, and then just calculate. So y2 is the y coordinate of the second point, which is 4, minus y1, which is 2, and then x2 minus x1 is the x coordinate of 2 minus the x coordinate of 1, so that's 2 minus 1. So what happens here is you just get 2 over 1, and so, therefore, the slope of a is just equal to 2. Alright? Another way you can kind of think about this 2 or this ₂ over 1 is what's the rise over the run. From this point to this point, how much did I rise by? I went from 2 to 4, so my rise is 2. And then what's the run? I went from 2 or sorry. I went from 1 over to 2 over here. So that means the run is just 1. So in other words, the rise over to run was just 2 over 1, and that's why we got a slope of 2. Let's do the exact same thing now for points for line b. Alright? So the slope is 2. So for line b, what we're going to do here is we're going to we're going to be in x1, y1, and x2, y2. Alright? Now in this case, the actual points aren't given to us already, so we're going to have to go pick them. And, basically, what you want to do here is you always want to pick points that are sort of, like, sit at the, sort of intersection of your grid. You don't want to pick points that are kind of, like, halfway in between a point because it's really hard to tell what numbers those are. So these are bad points. You're always going to look for points like this over here or this over here where you can very easily tell what those coordinates are. Alright? So in this case, this is going to be my x1, y1, and that's going to be my x2, y2. Alright? So what are those points? Well, this point over here is really just 4 comma negative one, and this point over here is really just 5 comma 4. Alright? So my x1y1 is 4, comma negative one, and this is just going to be 5, comma 4 over here. So let's use our equation now for the slope. So my MB is really just y2 minus y1 over x2 minus x1, or it's really just Δy over Δx. So let's try to use the rise over the run sort of technique. What's the rise in this equation? How much do I have to go up by before I go over? Well, look at this points. How much do I have to go up? I have to go 1, 2, 3, 4, and 5. So in other words, the Δy over here is 5. And what's the run? Well, I'm really just going from 4 to 5, so the Δx is just 1. Alright? So, really, without having to plug in all these points, you can just figure out that it's just 5 over 1 and the slope of this line is equal to 5. Alright. So let's take a look at these two numbers now. We got 2 and then we got 5 for the red line. So notice how I said earlier that the green line would be easier because it's a little bit shallower. Right? It's a little bit of an easier climb because not as steep, whereas the red line is way more vertical. Basically, what we can see here is that shallower lines have lower slopes, and steeper lines have higher slopes. So slope of 5 means you have to go up 5 before you can over go over 1. Alright? Now, one last point I want to make here is actually, you know, we picked these as our x1, y1 and x2, y2, but the order of points actually doesn't matter because it won't affect what your slope is. Generally, what's best to do though, is set your x1, y1 as the leftmost points. Basically, just because it's going to introduce the fewest amount of negative signs. Let me just show you what I mean by this. We're going to do this last example. We're basically going to recalculate this slope over here for a, but we're going to reverse the points. So now our x1, y1 is going to be 2, 4, and then our x2, y2 is going to be 1, 2. But we're going to see that the math works just the same way. So, our m a is just going to be y2 minus y1 over x2 minus x1. And, really, just what happens is if we're just going to use y2 minus y1, now this becomes 2 minus 4 divided by x2 minus x1. That's 1 minus 2. So 1 minus 2. Alright? And what we're going to see here that happens is we're going to get negative 2 over negative 1. The negatives actually cancel, and you still just end up with a slope of 2. So reversing the points actually doesn't affect the slope, but you just get a few more negative signs, and that's a little bit harder. Alright? So that's it for this one, folks. Thanks for watching.
Lines - Online Tutor, Practice Problems & Exam Prep
Created using AIUnderstanding the slope of a line is crucial in graphing and analyzing linear equations. The slope, represented as m, is calculated using the formula , indicating the steepness of the line. Lines can be categorized as positive, negative, zero, or undefined slopes. The slope-intercept form, y = mx + b, allows for quick graphing by identifying the slope and y-intercept. Recognizing parallel and perpendicular lines is essential, as parallel lines share slopes while perpendicular lines have slopes that are negative reciprocals of each other.
The Slope of a Line
Video transcript
Find the slope of the line shown below.
Find the slope of the line containing the points and .
Types of Slope
Video transcript
Everyone, in a previous video, we were introduced to slopes, which is the idea of the steepness of a line or a hill, or it's the rise over the run. Mathematically, it was ΔyΔx. Up until now, all the slopes that we've seen have been positive. What I'm going to show you in this video is that when you calculate slopes, it actually can fall into one of 4 categories. It can be positive or negative numbers, you can get a 0 slope, or you can get this new thing, which is called undefined. And I want to talk about each one of those things and show you the differences. So let's go ahead and take a look here.
Let's take a look at the line that we've already seen before, something that looks like this, and let's calculate the slope really quickly. So remember, I just need 2 points. Any two points work. It doesn't matter which ones I pick. So I'm just going to pick this one over here and this one. Remember, I can't use points like this because this is, like, halfway between a number, and that's bad. So, if I want to calculate the slope, the rise over the run between these two points, I just have to figure out how much I have to go up and then over. So my Δy is really just 2, and then I have to go over by 1. So my Δy is 2, my Δx is 1, and so I just get a slope of 2. Alright. We've seen that before.
Now let's take a look at the red line because the red line looks different. It doesn't look like this. It actually looks like this. So why does that look like that? Well, let's do the same thing and calculate the slope. I can just pick any two points. It doesn't matter which ones I pick. And it turns out that these actually all sort of fall on nice intersections of these two grids, so I can just pick any two points. It doesn't matter. What do I have to do to get from this point to this point? Well, in this case, instead of moving up, I have to go down. To get to the next point, instead of moving up like I did for this blue line, I have to go down. So mathematically, instead of a Δy being positive, the Δy is going to be negative. You're going to have negative 1, you have to fall 1, and then you have to go over by 1. So what's the ΔyΔx? Well, here, it's just going to be negative one over positive one, which is negative one. So, clearly, we can see here that the reason these two lines are different is because the signs of their slopes are different.
So, you have positive slopes, and it looks like this; negative slopes, and it looks like this. That's the difference. Let's take a look at a couple of other situations here. So, let's take a look at this purple line. This purple line is perfectly flat and horizontal. So, let's calculate the slope of this one. Well, if I pick any two points, again, it doesn't matter which points you pick. Let's just pick this one and this one over here. I want to calculate the ΔyΔx. What's the rise over the run of this line? Well, if you look at this, the rise is actually just nothing. I don't have to rise at all because it's perfectly flat. In other words, the change in the y-value is 0. So, the Δy is 0, but the Δx is the change in the x, and I've just gone over 2 in this situation. So here, my ΔyΔx is 0 over 2, and it actually doesn't matter what you plug in on the bottom of this equation because the slope will always be 0. So remember, the slope is the steepness of the line, and we got 0. That makes perfect sense because the steepness of 0 would just be a perfectly flat hill, and that's why the slope is 0.
So, let's take a look at this vertical line here, because the situation is a little bit similar. So, let's take any two points. I'm going to pick this point over here and this point. Again, I'm just picking them at random. Doesn't matter which ones you pick. What's the rise over the run? Well, in order to get from this point to this point, I have to rise by 3. That's my Δy. What about Δx? How much did you run over to get to the next point? Well, actually, you didn't because, again, we were here at x equals 2, and then, again, we're at x equals 2. So the Δx is just equal to 0. What this looks like is that your rise over the run is going to be 3 divided by 0. And this is just one of these weird math things that you can't do. We've talked about this before. You can never divide by 0. This is bad. So what we do here is we say that the slope of this line is undefined. It's a number that you can't really; it's actually not really a number. You can't define this because you can't divide by 0.
Vertical lines, the slopes are undefined. Whereas for horizontal lines, that's perfectly fine. That just means that your slope is equal to 0. Alright.
The last thing you have to know about these lines is their equations. Basically, when you have a horizontal line, it's going to look like y equals some number. For example, this perfectly flat horizontal line that we have here because all of the y-values are always 2, this equation is just y equals 2 no matter what the value of x is. So the general form of this equation is just going to be y equals some number. Sometimes textbooks will use the letter b for this. Then, for vertical lines, it's very similar. For this line, the x-value is always equal to 2 no matter what the y-value is. So, vertical lines will always have x equals some number, and I think, usually, textbooks use the letter a for this.
That's going to be important to know, just knowing those two forms of equations. Anyway, thank you for watching. That's it for this one.
Graph a line with a slope of 0 that passes through the point .
Which of the following graphs below represents the equation ?
Slope-Intercept Form
Video transcript
Hey, everyone. So throughout our discussion on lines, we've seen problems where they ask us to calculate the slope of a line by looking at the rise over the run between two points. But some problems like the one we're going to work out down below won't ask for just that. Some problems will ask us to look at the graph of a line and write its equation in a very specific way called the slope-intercept form. So that's what I want to talk about in this video. And what I'm going to show you is it's basically just a very specific way that we write an equation of two variables using two things we've already seen before independently. So we can use its slope and its intercept, specifically the y-intercept. Alright? So I'm going to show you this equation, and it's probably something that you've seen before. So let's get started.
The slope-intercept form of an equation is actually just an equation. That's y=mx+b. You've probably heard that at some point in a math class, y=mx+b. This is just the slope-intercept form of a line. It's one of the most easy and straightforward ways to describe a line equation. So let's get started and talk about these two variables here. The m is basically just the slope, and we've already seen that before. We calculate that by using ΔyΔx, rise over run, or you can just use the sort of longer format here. So in this equation, what we can see is that the rise over the run between these two points is 2 over 1, and so the slope is just 2. What about the y-intercept? Well, the b term over here is the y-intercept, and we've already talked about that separately. The y-intercept is basically just the y value wherever the graph crosses the y axis, and it's where x=0. So for instance, in this case, the graph crosses the y axis right over here. The y value at this point is 3. So that is the b term. Right? So that's the y-intercept. So to put these things together, y=mx+b, all you have to do is the equation here has a slope of 2, so that goes in front of the x, and then the intercept is 3. So the equation of this line is just y=2x+3. That's how to describe this equation in slope-intercept form. That's really all there is to it. Alright? So that's all there is to slope-intercept form. Let's go ahead and take a look at another example. Alright? So in this graph below, we're going to identify the slope, sorry, the slope and the y-intercept, and then we're going to write the equation in slope-intercept form. So remember, slope-intercept form here is just going to be y=mx+b. In order to figure out m and b, we're going to have to take a look at the graph. Alright? So the always easiest sort of value to start with is going to be the b term because you really just have to look at the graph and figure out where does it cross the y-axis. You don't have to calculate anything. So let's take a look at this graph. Where does it cross the y-axis? Well, it crosses right over here. So what's the y value where this graph crosses the y-axis? It's just negative 3. So that's the b. It's just negative 3. That's all there is to it. You don't have to write the ordered pair. It's just the y value. Alright? So how do we calculate m? Well, for m, we're going to have to use rise over run. So we're going to m we're just going to calculate this by using ΔyΔx. Or if we're given two points, you could just plug those points in. But, basically, if I'm going to have this point ove
In the graph shown, identify the y–intercept & slope. Write the equation of this line in Slope-Intercept form.
Graphing Lines in Slope-Intercept Form
Video transcript
Hey, everyone. So in a previous video, we were introduced to the slope intercept form of a line, y=mx+b. And we saw some problems where a graph of a line was already given to us, and we wanted to write the equation in slope intercept form. But in some problems, like the one we're going to work out here, you actually will do the opposite. You'll have the equation that's already given to you, and you'll be asked to graph it. So that's what I'm going to show you how to do in this video, how to graph lines when you're given the equations in slope intercept form. And, basically, what I'm going to show you is that a line equation in this form tells you everything that you need to graph it very quickly. And I'm going to show you a step by step way to do that. So let's just jump right into our example and get started here. So we have the equation y=23x+1, and the first thing we want to do is we want to identify the y-intercept and then the slope over here. So let's get started. Remember, the y-intercept is just the b term in y=mx+b. So if you look at this equation, y=23x+1, what you'll see here is that the b is basically just the 1. It's the thing that's constant at the end, and the m is just the slope. It's the thing that goes in front of the x, which is 23. So right from this equation, we could just immediately pull out the fact that the b term is just 1. That's the y-intercept, and the slope is just a fraction, which is 23. So how do we graph this? Well, the first thing you're going to do is you're just going to plot the y-intercept. That's the easiest thing to plot because you don't have to calculate anything. You're just sort of marking a place on the graph. The y-intercept is the y value where it crosses the y axis, so I know that this graph is going to cross through this point. But that's not enough information to graph this because I don't know if it's going to look like this or this or that, so I'm going to need more points. So that actually brings us to the second step here, which is we're going to plot at least one more additional point, and the way we do that is by using the definition of slope. Remember, slope is just rise over run. So in other words, we have to go rise 2, and then we have to run over by 3 in order to get to the next point. So, basically, you're going to take your y-intercept here, and you're just going to go up 2. You're going to rise 2, and then you have to go over 3. Just do rise over run to get to the next point. You can either go up to the right or you could go down to the left. All you really need is just one additional point. Now once you've done that, now you're basically done because all you have to do is just connect the points with a line. So, again, you could have gone downwards like this, and this basically would have just gone down 2 and over 3. But, anyways, you would actually end up seeing that the equation of your line kind of goes through all three of these points, and it looks something like this. Alright? So that's how we go from an equation to a graph in 3 simple steps. Hopefully, that made sense. Thanks for watching.
Identify the 𝒚– intercept & slope of . Then graph the equation.
Point-Slope Form
Video transcript
Hey, everyone. So in earlier videos, we saw the slope intercept form of a line, \( y = mx + b \). And usually, we use this form whenever we were given information about the slope and intercept and asked for the graph of the equation or the other way around. So, for example, we were asked to graph something like \( y = \frac{2}{3}x - 1 \). What I'm going to show you in this video is that sometimes you might be given an entirely different set of information. You might be told something like a slope, and then it passes through some point. So when you're asked to write an equation of a line that passes through a point that is not the y intercept, I'm going to show you that we actually use a different form of writing an equation called the point-slope form. Now I'm going to show you the differences and similarities between the two equations. So let's go ahead and get started here.
Again, I first want to talk about when you use these two different forms. We use \( y = mx + b \) whenever we're given information about \( m \) and \( b \) and ask for the graph or the other way around. So, for example, \(\frac{2}{3}x - 1\), we're given the \( m \) and the \( b \), and we're asked to graph it. And we can see how to do that very quickly here. We just know that it's going to pass through the point (0, -1). That's the y intercept, and then we just sort of graph the next point by using rise over run. The slope is \(\frac{2}{3}\), so you go up 2 over 3. And, basically, this line is going to look something like this. Alright. Now let's take a look at the equation the example that we're going to figure out solve here, which tells us that we're going to have to write the equation of a line that has a slope of \(\frac{2}{3}\), and it passes through some random point (3, 1).
So, basically, whenever you're given information like this, whenever you're given the slope like we have here and some random points, which is going to be something like \( (x_1, y_1) \), then you're going to use this new form called the point-slope form. You also could be given 2 points of information like \( (x_1, y_1) \) and \( (x_2, y_2) \). Alright? So that's the times where you're going to use this new point-slope form. And, basically, it's \( y - y_1 = m(x - x_1) \). So, really, with this equation, there are three numbers that you need to plug into this equation because these y's and x's actually don't get replaced with numbers. Alright? And so the reason we call it a point slope is because \( x_1 \) and \( y_1 \) really are just a point that it's giving you.
So let's get started here with part a. We're going to write the equation in this new form. So I'm going to take this equation here, \( y - y_1 = m(x - x_1) \). So I first need the slope of the line, and so I'm going to go ahead and figure that out first. And we are actually already told directly what the slope of this line is. It's just \(\frac{2}{3}\). So we already have what that number is. So now all we need to do is just figure out the \( x_1 \) and the \( y_1 \). So what is that? Well, really, it's just the point that they're telling you that it passes through. When they say that it passes through the point (3, 1), what they're saying is that this line is going to pass through this point on the graph over here. That's just a coordinate. It's just they're really just giving you the \( x_1 \) and \( y_1 \) that you plug into the equation. So it's really straightforward. You just take these numbers and just pop them right into this equation over here, and you're basically done.
So if I want to just rewrite this equation, this is going to be \( y - 1 = \frac{2}{3}(x - 3) \). Alright? So this is the equation in point-slope form of the line that passes through this point over here and has a slope of \(\frac{2}{3}\). That's it. That's the point-slope form. Alright? So we're basically done with part a. Now in part b, we're going to graph the line. So how do we do this? Well, again, we know this line is going to pass through this point (3, 1), but that's not enough for me to build the line because there's only one point. So the way we did this for slope intercept form was once we got the y intercept, we got the next point by using the slope. That's a very similar idea here. We know it passes through this point over here, so I can get the next point by using the rise over run in the slope. So I can go up 2 and over 3, and I'll end up over here, or I can go down 2 and to the left 3, I'm going to see that it passes through this point. So if I connect those points with a line, it's going to look something like this over here.
Now if you look at these two equations or these two graphs that we've ended up with, we've actually ended up with the exact same line. So, basically, what happens is that this equation over here, \(\frac{2}{3}x - 1 \), and this equation that we wrote in point-slope form are actually the same exact equation written in 2 different ways. And the way I'm going to show that to you is we're going to use we're going to go through part c. We're going to rewrite my equation in slope intercept form. Alright? So how do I take this equation and now write this in \( y = mx + b \)? I basically just have to solve and isolate for this y term over here. So let's do that. I've got \( y - 1 = \frac{2}{3}x - 2 \). So if I want \( y \) by itself, first, I'm going to have to distribute the \(\frac{2}{3}\) into everything that's inside the parentheses. So I get \( y - 1 = \frac{2}{3}x - 2 \). So, now the last thing I have to do is just add 1 to both sides over here. Whatever you do to one side, you have to do to the other. And so I just get \( y = \frac{2}{3}x - 1 \). So notice how now this is in slope-intercept form, and we've basically just gotten right back to the equation that we had on the left. So again, these two graphs over here and these two equations mean the exact same thing, but they're just written in 2 slightly different ways. Alright? So, hopefully, that made sense. Hopefully, you understand the difference between slope intercept and point-slope form. Let me know if you have any questions. Thanks for watching.
Write the point-slope form of the equation of a line with a slope of that passes through (1, 3). Then graph the equation.
Write the point-slope form of the equation of a line with a slope of that passes through . Then graph the equation.
Finding Equations of Lines Given Two Points
Video transcript
Hey, everyone. So, in previous videos, we saw how to write equations in point-slope form whenever we were given information about the slope and a point that the line passed through \(x_1, y_1\). What I'm going to show you is that in some problems like this one we're going to work out down here, sometimes you won't be given the slope, that \(m\) value, and instead, you'll be given information about 2 of the points. And what I'm going to show you is that we're still going to use the point-slope form for this, and it's actually going to turn out to be very similar to the problems we've already done before, but there's just one extra step. So let's go ahead and get started here. Alright?
So, I just want to remind you that we're not going to use the slope-intercept form \( y = mx + b \) for these types of problems because in those problems, we're usually given some information about \(m\) and \(b\), and we're asked for the graph, or you're asked for \(m\) and \(b\). We're not told anything about the y-intercept in this kind of problem. All we're told through is that it passes through these two points, \((-1, -5)\) and \((2, 4)\). So we don't use \( y = mx + b \), and instead, we're still going to use the point-slope form because we have some information about the points. So I'm going to write my equation \(y - y_1 = m (x - x_1)\). Remember, this equation, I need three numbers here. I need \(y_1\), \(x_1\), and I need the slope. Now in some problems, the slope was already given to us in previous problems, but in this case, it actually wasn't. So because we don't know what \(m\) is directly, we want to go find that first. So how do I go and calculate \(m\)? Well, remember that the \(m\) is really just the slope. It's the rise over the run. So, basically, you just use these two equations over here, \(\Delta y / \Delta x \) or \(y_2 - y_1 / x_2 - x_1\). So I'm going to use this \(y_2 - y_1 / x_2 - x_1\) because I'm told information about 2 of the points, and I don't have these things sort of graphed out already. Alright? So remember, I want to pick my points so that the \(x_1, y_1\) is the leftmost point. Again, it doesn't matter which point you pick. It'll still be the same no matter what. So this is going to be my \(x_1, y_1\), and this is going to be my \(x_2, y_2\). Alright? So here, what I've got here to calculate the slope is \(y_2 - y_1\). So, in this case, I've got \(4 - (-5)\). So I've got \(4 - (-5)\) over here, and then I've got divided by \(x_2 - x_1\). So this is going to be \(2 - (-1)\). \(2 - (-1)\). What I end up getting over here is I'm getting \(9/3\), which actually just gives me an \(m\) of \(3\). So that's my \(m\) term over here. I've got what my slope is, and I'm just going to pop that right back into this equation. But I'm not done yet because now I just need my \(x_1\) and \(y_1\). Now again, it doesn't matter which point you pick as your \(x_1, y_1\). So you can use these numbers and pop them into this equation over here for \(x_1, y_1\), or you could use these. It really just depends on which ones you picked. Now because I've already picked my \(x_1, y_1\) to be these numbers, I'm just going to go ahead and use these numbers. Okay?
So what I'm going to do here is I'm going to do \(y - (-5) = 3(x - (-1))\). And if I go ahead and sort of just draw a little box around this, this actually ends up being my final equation. So this is the equation of this line that passes through the points, and that's really all there is to it in point-slope form. Again, if you use these numbers, you would have gotten a slightly different form, and that's perfectly fine because it actually ends up being the same equation. So now, what we're going to do is we're just going to graph this. Alright? Well, graphing this is actually pretty straightforward because remember, we always need 2 points to graph a line, and we already know what they are. This is just \((-1, -5)\) and then \( (2, 4) \) over here. So all you have to do is just connect these lines or connect these points with a straight line like this. If you have a straight edge, that's even better. But this is really all there is to it. So first, you just get the slope by plugging into our slope equation, and then you just pick either one of the two points. Alright? So that's really the big idea here is that whenever you're given 2 points, you can just use either one of the two points that you're given as \(x_1\) and \(y_1\). It won't matter. Alright? So that's it for this one, folks. Let me know if you have any questions.
Write the point-slope form of the equation of a line that passes through the points and . Then graph the equation.
Standard Form of Line Equations
Video transcript
Hey, everyone. So throughout our discussion on lines, we've seen equations and lines in different forms, like slope-intercept or point-slope form. But you might be given a problem with an equation that looks like this, with all the terms of x and y on the left side. What I'm going to show you in today's video is that this is just another way of writing an equation of a line. This is called the standard form. I'm going to show you what it's helpful for, but most of the time in problems, you're going to be able to take this equation and rewrite it in one of the forms that we already know, like slope-intercept. So I'm going to show you that these two equations actually mean the exact same thing. They're just written in slightly different ways. Alright? Let's get started here.
So if you take a look at our problem, what we're going to do is we're going to find the slope and the y-intercept, which we already know how to do. But of this equation over here, -9x + 3y - 120 = 0, it doesn't look anything like the forms that we already know. So the standard form, the way that these equations are generally written, is like ax + by + c = 0. So clearly, we can see here that this is like a, b, and c, and this equals 0. So instead of having m's and b's, these are really just coefficients that stand for the numbers inside of your equation. Alright?
So how do I solve this problem? I have a's, b's, and c's, but I'm asked for the slope and the intercepts. Remember that the slope is just m, so that's what I want to find, and I want to find b over here. How do I find that from this equation over here? Well, basically, what happens is whenever you're given a problem in standard form, like we have here, and you're asked for the slope or the intercept, you're going to have to rewrite this equation. And the way we rewrite the equation is by isolating and solving for y to the left side of the equation. Alright?
So I'm going to take this equation over here and to convert it into y = mx + b, I'm going to have to rewrite it so that y is on the left side. Alright? So I'm going to take this -9x, and I have to move it over to the right side and have to add 9x, and I have to take the -12 and also move it over and add 12. So I have to take everything and move it to the right side. What happens is the 3y just stays behind on the left side. I get 3y = 9x + 12. Alright? Now we're not done yet because this still doesn't look like y = mx + b. I have to get rid of the 3, and the way that I do that is by dividing it out. So I have to divide each number in the equation by 3. So the 3 goes away on the left side, and all I'm left with is y. And then what here happens with 9 over 3 is it just turns it to 3, and then 12 over 3 just becomes 4. So this is the equation now that I've ended up with, y = 3x + 4. And if you look at this, this actually is in slope-intercept form. Right? I've got y = mx + b. So these are the two numbers. I've got 3 and 4, and I'm basically done here. Those are the numbers I'm looking for. My slope is equal to 3, and my y-intercept is equal to 4. So that's the answer to this problem. These equations over here and this one mean the exact same thing. They're just written in slightly different ways. Alright? Okay.
So that's one of the cases where you use the standard form. It's basically when you're just asked to rewrite it in a different form. But what I'm also going to show you right now is it's also really helpful in finding the x and y intercepts. So let's go ahead and take a look at our next example over here.
So you might be given a line that's written in standard form like this 3x + 2y - 6 = 0, and you might have to find the intercepts without first converting it back to slope-intercept form. Alright? So I'm going to show you how to do that. To graph a line in standard form, you can find these intercepts very quickly without rewriting it in slope-intercept. And basically, let's just recall what these intercepts actually mean. Remember that the intercept, the x intercept, is where it crosses the x-axis, and it's where the y value is equal to 0. And the opposite happens for the y intercept. That's where the x value is 0, and that's where it crosses the y-axis. So what we're going to do here in this problem is we're going to take this equation over here, and we're going to set the y and x equal to 0 and solve. Let's go ahead and do this for the x intercept. Right? So if I want the x intercept, what I'm going to do is I'm going to rewrite this equation, 3x + 2y - 6 = 0, and I'm going to set y equal to 0, and then I'm just going to solve for x. So, in other words, I'm going to take this 3x, and I'm just going to replace y with 0, in which that whole term now just goes away. And now all I have to do is I have an equation of one variable, and I just solve for x. So how do I do that? Well, I'm going to bring the 6 over to the other side. So this just becomes 3x = 6 and x = 2. So that's my x intercept. Right? I just solve for x. What that means is if I go over my graph here, I can say that I know this graph crosses the x-axis at x equals 2, but that's not enough to graph the line because it's only one point. So now we have to do the exact same thing, but now for the y intercept. And once we have these two points, then we can go ahead and connect them and form our line. So with the y intercept, I'm going to do the exact same thing, 3x + 2y - 6 = 0. But now what I'm going to do is do the opposite. I'm going to set x equal to 0 over here, and I'm going to solve for y. So what I have to do is I have to replace the x with 0, and that term just goes away. So this is, 2y - 6 = 0. And now I just move the 6 over, like I did the other side. So that's plus 6, and I ended with 2 y = 6. And if you figure this out, this is going to be y = 3. So these are my x and y intercepts. I've got x equals 2 and y equals 3. So that's this point over here. Now we have the two points of our line, so we can actually just connect them, and that's going to form our line segment. So I just connect these two points using a ruler or a straight edge or something like that, and that's going to be the equation of my line. I'm just going to move it over a little bit. There we go. So this is the equation of my line, and I got that without having to convert it to slope-intercept form. Alright? So, hopefully, that made sense. Thanks for watching.
Find the slope & of the line given by the equation
Graph the equation by finding the intercepts.
Parallel & Perpendicular Lines
Video transcript
Hey, everyone. So in previous videos, we've seen the three different ways of writing line equations in three different forms. Well, some problems, like the one we're going to work out down below, will give us an equation in any one of these forms and ask us to write lines that are parallel or perpendicular to those lines. That's what I want to show you in this video. We're going to see that parallel and perpendicular lines are really just related by the values of their slopes. Alright? So let's go ahead and take a look here.
I've got these two graphs, and I've got these two lines in this diagram over here, -3x + 2 and -3x - 4. You can see that they're graphed here. Well, if you notice that these lines are sort of, like, perfectly almost identical, they're just sort of shifted, you know, to the side. And that's the key characteristic of parallel lines. The key characteristic is that because they're sort of exactly the same and just shifted over, they actually never intersect. And that really just has to do with their slopes. Notice how the slopes here are both negative 3. So for parallel lines, the slopes are always equal to each other, and the y-intercepts are different. So in other words, they both have a slope of negative 3, but their y-intercepts are different, like 2 and negative 4. If both of these things were the same, it would actually just be describing the exact same line. So the key characteristic for parallel lines is the slopes are equal and the b's or the y-intercepts are different. Alright?
If these two things have the same slope, it's basically like the rise over the run of each of these points will always be the same, and they'll never cross each other. Alright? Now let's take a look at perpendicular lines. Here, what I've got is I've got -3x + 2. I've got the exact same lines I had over here, but now the other line, this orange one over here, has \frac{1}{3}x - 4. So, clearly, these two things have very different slopes and y-intercepts, and we can see that they do actually intersect. Now what's special about perpendicular lines is that the point where they intersect is they intersect at right angles. So in other words, this sort of this intersection point over here has an angle of 90 degrees. That's what perpendicular actually means. And, basically, what you need to know about these lines is that the slopes here are different. So the negative three is the slope of the one line, and then we have \frac{1}{3} for the slope of the other. These things are related, because notice how one is positive or sorry. One's negative and the other one's positive, and they're also reciprocals of each other. That's actually always what's going to happen between perpendicular lines. The slopes will always have opposite signs. So in other words, one was positive and one was negative, and they're also going to be reciprocals of each other. So you're basically just going to flip the fractions or whole numbers or something like that. Alright? So that's basically the difference between parallel and perpendicular lines. You may see some symbols regarding these things. You may see some, like, sort of kind of like to remember way I kind of like to remember it is that parallel lines have the symbol, and it kinda looks like the double l that's inside the word. Alright? So just in case you see that. That's basically the difference. Let's go ahead and take a look at some, example problems. Alright?
So here, what we want to do is we want to write an equation of a line that passes through a point and is parallel to some other reference line that it's giving us, y = 2x - 6. So in other words, I want to write an equation of a line that is parallel to this line over here. So parallel means that I want to have an equal slope and a different y-intercept. So in other words, I'm looking for a line in which the slope is equal to 2 because that's the slope of this line, m = 2. So it has to be the same. Alright? Now notice how this problem actually hasn't told us what form of an equation to write, and that's what we're going to have to figure out. But notice how this problem tells us that we also are going to be passing through a point. That's the equation of our line. So we're going to be passing through the point (-1, 4). And if you remember, what happens is if you're ever given the slope and a point, we always write the equation using point-slope form. So we're going to write the equation in point-slope. Alright? So I'm just going to write that out for a second. Basically, what we're going to do here is we're going to write y - y_1 = m (x - x_1). Alright. So this is the sort of now we just have to fill in the so the sort of variables. And remember the y_1 and x_1 just have to do with the point that we picked, which is (-1, 4), and the m is just the 2. So just gonna fill this out really quick. I'm gonna do the y_1, which is 4, so y - 4 = m (x - (-1)). Remember these are variables, and we don't replace them with numbers. Alright? So all we have to do is just clean this up a little bit, but this is gonna be y - 4 = 2 (x + 1). Alright? So this is the equation of a line that passes through the point (-1, 4) and is parallel to this equation over here because they have the same ms. And, in fact, if you graph these two equations out, what you're going to see is we're going to have 2x - 6, which kind of looks like, this over here passes through negative 6 and has a slope of 2. And then if you graph this point over here, we know that it's going to pass through the point (-1, 4), and it's also going to have a slope of 2. So if you draw some points out and connect them, we're going to see sort of as a rough sketch that these two lines are parallel to each other. They will never intersect. Alright.
Let's take a look at our next problem here. Here, we have to write the equation of a line that is now perpendicular. So we're looking for a line that is perpendicular to this equation over here that's written in standard form, and it has a y-intercept of 3. So what are we told? We're told that it has a y-intercept, which remember b, so b = 3. Alright? So remember which so first, we have to figure out what form we're going to write this equation in, And remember that whenever we're given a b term or asked for b, we're always going to write this in slope-intercept form. Right? So if we're given or asked for b, we write it in slope-intercept form. Okay. So if I want to write slope intercept form, I need the b, which I have, but I also need the m. So that m that I need has to be perpendicular to this line over here. In fact, what I'm actually going to do is I'm going to write this over here for seconds. So I have to have an m that is perpendicular to this line, which is in standard form. So to figure that out, first, I'm going to have to sort of isolate and solve for this y over here. What I'm going to do is I'm going to take this x, move it over, and the negative 8 and move it over. I'm going to have to subtract x, and I'm going to have to add eights from both sides. Alright? So this ends up going away, and I end up with 4y = -x + 8. Now what I have to do is I have to divide by 4 of each one through each one of the terms over here, and I get rid of the 4. So this is going to be y = -\frac{1}{4}x + 2. So remember, this is the equation not that I'm trying to find. This is the equation of this line over here just written in standard form. And I needed to write in standard form because I needed to figure out what the m is. Alright? So this m is -\frac{1}{4}. To get an m of my line that I'm trying to find, I have to do the opposite sign and the reciprocal of this number. The opposite sign is going to be a positive, and the reciprocal of this number is going to be an m that's equal to 4. So now that I have m and b, now I can go ahead and write the equation of my line that is perpendicular. So this is going to be y = mx + b. So in other words, this is going to be y = 4x + 3. So let's graph these lines and see if we've actually done this correctly. So this is an equation y = -\frac{1}{4}x + 2. So it starts here, and we go down 1 and over 4, up 1 and to the left 4. So this line is going to kind of look like this. Now our line is going to look like 4x + 3. So that's an equation that starts here, and it has a slope of 4. So we go up 4 over 1 or down 4 and then over 1, down 4 over 1. So this line is going to look kind of like this. And if you look at these two lines over here, they intersect at this point, and the intersection is definitely 90 degrees. Alright?
So that's it for this one, folks. Hopefully, this made sense. Thanks for watching.
Write an equation of a line that passes through the point and is parallel to the line .
Here’s what students ask on this topic:
What is the slope of a line and how is it calculated?
The slope of a line, represented by the variable , measures the steepness or incline of the line. It is calculated using the formula , where and are the y-coordinates of two points on the line, and and are the x-coordinates of those points. This formula essentially measures the change in the y-values (rise) divided by the change in the x-values (run). A positive slope indicates the line rises as it moves from left to right, while a negative slope indicates it falls.
Created using AIWhat are the different types of slopes a line can have?
A line can have four types of slopes: positive, negative, zero, and undefined. A positive slope means the line rises from left to right, indicating an upward trend. A negative slope means the line falls from left to right, indicating a downward trend. A zero slope means the line is horizontal, indicating no vertical change as it moves along the x-axis. An undefined slope occurs when the line is vertical, meaning there is no horizontal change, and the denominator in the slope formula is zero, which makes the slope undefined.
Created using AIHow do you write the equation of a line in slope-intercept form?
The slope-intercept form of a line's equation is , where represents the slope and represents the y-intercept, the point where the line crosses the y-axis. To write the equation, you need to determine the slope and the y-intercept . For example, if a line has a slope of 2 and crosses the y-axis at 3, the equation would be .
Created using AIWhat is the difference between parallel and perpendicular lines?
Parallel lines have the same slope but different y-intercepts, meaning they never intersect and are always the same distance apart. For example, the lines and are parallel. Perpendicular lines intersect at a right angle (90 degrees). Their slopes are negative reciprocals of each other. For example, if one line has a slope of , a line perpendicular to it will have a slope of .
Created using AIHow do you graph a line given its equation in slope-intercept form?
To graph a line given its equation in slope-intercept form , follow these steps: First, plot the y-intercept on the y-axis. This is the point where the line crosses the y-axis. Next, use the slope to determine the rise over run from the y-intercept. For example, if the slope is , move up 2 units and 1 unit to the right to plot the next point. Finally, draw a straight line through these points to complete the graph.
Created using AI
