Ch. 3 - Polynomial and Rational Functions

Blitzer8th EditionCollege AlgebraISBN: 9780136970514Not the one you use?Change textbook

Blitzer 8th Edition

Ch. 3 - Polynomial and Rational Functions

Problem 12

Chapter 4, Problem 12

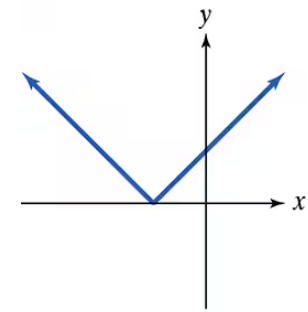
Identify which graphs are not those of polynomial functions.

Verified step by step guidance

Step 1: Observe the shape of the graph. The graph shows a V-shaped function with two straight lines meeting at the origin (0,0).

Step 2: Recall that polynomial functions are smooth and continuous with no sharp corners or cusps. Their graphs are made up of curves, not sharp angles.

Step 3: Notice that the graph has a sharp corner at the origin, which indicates a cusp or a point where the function is not differentiable.

Step 4: Recognize that this V-shaped graph resembles the absolute value function, which is defined as $y = |x|$, and is not a polynomial because it involves an absolute value operation.

Step 5: Conclude that since the graph has a sharp corner and is not smooth, it is not the graph of a polynomial function.

Verified video answer for a similar problem:

This video solution was recommended by our tutors as helpful for the problem above.

Video duration:

48s

Was this helpful?

Key Concepts

Here are the essential concepts you must grasp in order to answer the question correctly.

Polynomial Functions

Polynomial functions are algebraic expressions consisting of variables raised to non-negative integer powers with constant coefficients. Their graphs are smooth and continuous curves without sharp corners or cusps, and they can have turning points but no abrupt changes in direction.

Graph Characteristics of Polynomial Functions

The graphs of polynomial functions are continuous and differentiable everywhere, meaning they have no sharp points or corners. They typically exhibit smooth curves, and their end behavior depends on the leading term's degree and coefficient.

Non-Polynomial Graphs and Sharp Corners

Graphs with sharp corners or 'V' shapes, like the absolute value function, are not polynomial functions because polynomials are differentiable everywhere. Such graphs indicate piecewise or non-polynomial functions, which have points where the derivative does not exist.

Recommended video:

05:25

Graphing Polynomial Functions

Related Practice

Textbook Question

In Exercises 9–16, a) List all possible rational zeros. b) Use synthetic division to test the possible rational zeros and find an actual zero. c) Use the quotient from part (b) to find the remaining zeros of the polynomial function. f(x)=2x³−3x²−11x+6

449

views

Textbook Question

Use the graph of the rational function in the figure shown to complete each statement in Exercises 9–14.

As $x \to - \infty, f (x) \to_{_{}}$ _____

Divide using long division. State the quotient, and the remainder, r(x). (x⁴−81)/(x−3)

549

views

Textbook Question

Identify which graphs are not those of polynomial functions.

1037

views

Textbook Question

Solve each polynomial inequality in Exercises 1–42 and graph the solution set on a real number line. Express each solution set in interval notation. 9x²+3x−2≥0