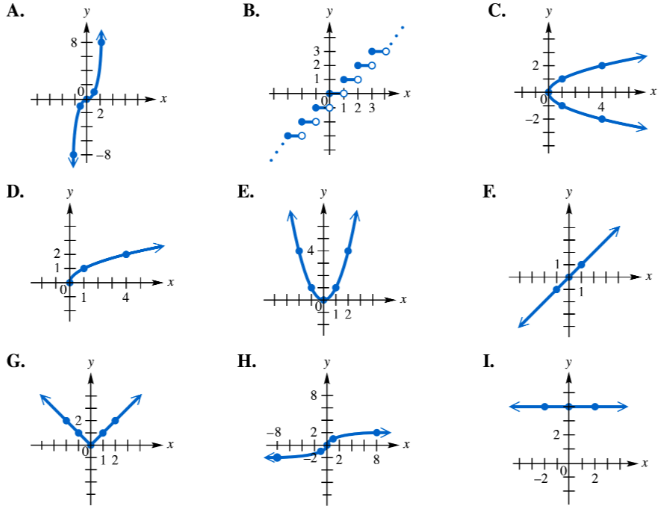
To answer each question, refer to the following basic graphs. Which one is the graph of ƒ(x)=|x|? What is the function value when x=1.5?

Verified step by step guidance

1. Recognize that the function ƒ(x) = |x| represents the absolute value of x, which means the output is always non-negative regardless of whether x is positive or negative.
2. Understand the shape of the graph of ƒ(x) = |x|: it forms a 'V' shape with its vertex at the origin (0,0), where the graph decreases linearly for x < 0 and increases linearly for x > 0.
3. Identify the graph among the given options that has this characteristic 'V' shape with the vertex at the origin, confirming it is the graph of ƒ(x) = |x|.
4. To find the function value when x = 1.5, substitute 1.5 into the function: ƒ(1.5) = |1.5|.
5. Since the absolute value of a positive number is the number itself, the function value at x = 1.5 is simply 1.5.

Key Concepts

Absolute Value Function

The absolute value function, denoted as ƒ(x) = |x|, outputs the non-negative value of x. It transforms any negative input into its positive counterpart, making the graph V-shaped with a vertex at the origin (0,0). Understanding this function is key to identifying its graph and evaluating values.

Graph Interpretation

Graph interpretation involves recognizing the shape and key features of a function's graph. For ƒ(x) = |x|, the graph consists of two linear pieces joined at the origin, sloping upward on both sides. Identifying this shape helps distinguish it from other basic graphs.

Function Evaluation

Function evaluation means substituting a specific input value into the function to find the output. For ƒ(x) = |x|, evaluating at x = 1.5 involves calculating the absolute value of 1.5, which is 1.5. This process confirms the function's behavior at given points.