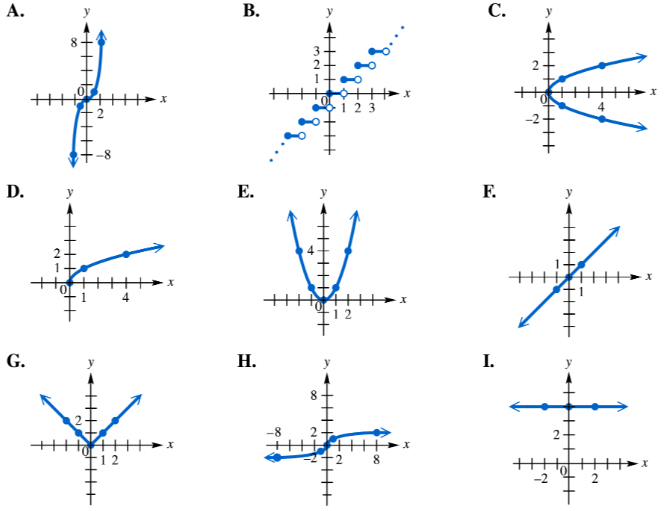
To answer each question, refer to the following basic graphs. Which one is the graph of ƒ(x)=x²? What is its domain?

Verified step by step guidance

1. Identify the function given: ƒ(x) = x^2 is a quadratic function, which graphs as a parabola opening upwards.
2. Recall the shape of the graph of ƒ(x) = x^2: it is a U-shaped curve with its vertex at the origin (0,0).
3. Look at the provided basic graphs and select the one that matches this U-shaped parabola with vertex at the origin.
4. Determine the domain of ƒ(x) = x^2: since you can input any real number for x and get a real output, the domain is all real numbers.
5. Express the domain in interval notation as \((-\infty, \infty)\), meaning x can be any real number.

Key Concepts

Quadratic Functions

A quadratic function is a polynomial function of degree two, typically written as f(x) = x². Its graph is a parabola that opens upwards, symmetric about the y-axis, with the vertex at the origin (0,0). Recognizing this shape helps identify the graph of f(x) = x².

Graph Interpretation

Graph interpretation involves analyzing the shape, position, and key features of a graph to match it with a given function. For f(x) = x², the graph is a U-shaped curve, and understanding these visual cues is essential to correctly identify the function's graph.

Domain of a Function

The domain of a function is the set of all possible input values (x-values) for which the function is defined. For f(x) = x², the domain is all real numbers since any real number can be squared without restriction.