To answer each question, refer to the following basic graphs. Which one is the graph of ƒ(x)=x3? What is its range?
Table of contents
- 0. Review of Algebra4h 18m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations1h 43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 5m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 22m
- 10. Combinatorics & Probability1h 45m
3. Functions
Intro to Functions & Their Graphs
Problem 11
Textbook Question
Determine the intervals of the domain over which each function is continuous.
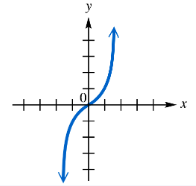
 Verified step by step guidance
Verified step by step guidance1
Step 1: Understand the concept of continuity. A function is continuous on an interval if there are no breaks, jumps, or holes in the graph over that interval. Mathematically, a function f(x) is continuous at a point x = a if the limit of f(x) as x approaches a equals f(a).
Step 2: Examine the graph carefully. Notice the point (2, 0) where the graph has a filled dot, indicating the function is defined at x = 2 with value 0. Check if the graph is connected without breaks on either side of this point.
Step 3: Identify any discontinuities. Look for any jumps, holes, or vertical asymptotes. In this graph, the curve appears smooth and connected on both sides of x = 2, with no breaks or jumps.
Step 4: Determine the intervals of continuity. Since the graph is continuous everywhere shown, except possibly at x = 2, and the function is defined and connected at x = 2, the function is continuous over the entire domain shown.
Step 5: Express the domain intervals. Based on the graph, the function is continuous on the interval from negative infinity to positive infinity, or in interval notation: \((-\infty, \infty)\).
 Verified video answer for a similar problem:
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
1mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Continuity of a Function
A function is continuous at a point if the limit of the function as it approaches the point equals the function's value at that point. This means there are no breaks, jumps, or holes in the graph at that point. Continuity over an interval means the function is continuous at every point within that interval.
Recommended video:

Graphs of Common Functions
Limits and Their Role in Continuity
The limit of a function at a point describes the value the function approaches as the input approaches that point. For continuity, the left-hand limit and right-hand limit at the point must be equal and match the function's value there. Limits help identify points of discontinuity when these conditions fail.
Recommended video:

Interval Notation
Types of Discontinuities
Discontinuities occur when a function is not continuous at a point. Common types include removable discontinuities (holes), jump discontinuities (sudden jumps in value), and infinite discontinuities (vertical asymptotes). Identifying the type helps in understanding the behavior of the function and its domain of continuity.
Recommended video:
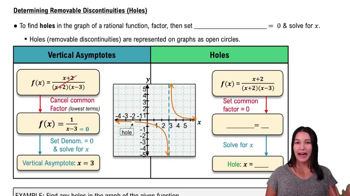
Determining Removable Discontinuities (Holes)

 5:2m
5:2mWatch next
Master Relations and Functions with a bite sized video explanation from Patrick
Start learningRelated Videos
Related Practice
Textbook Question
557
views
