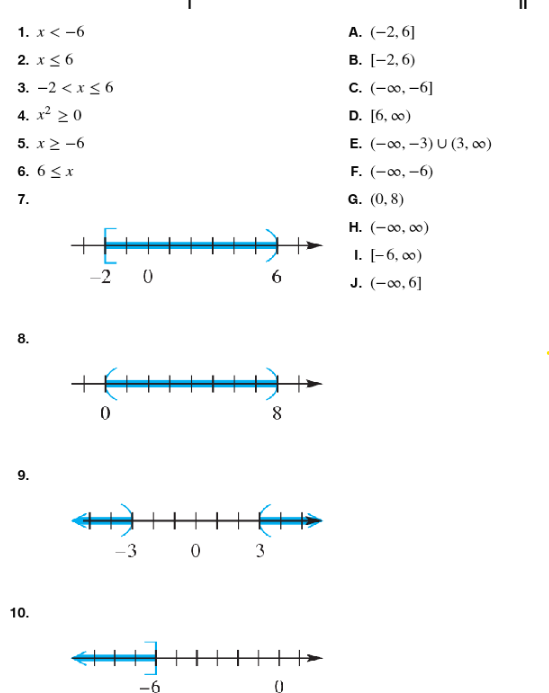
Match the inequality in each exercise in Column I with its equivalent interval notation in Column II. -2 < x ≤ 6

Verified step by step guidance

1. Identify the inequality given: \(-2 < x \leq 6\). This means \(x\) is greater than \(-2\) but less than or equal to \$6$.
2. Recall that interval notation uses parentheses \(()\) for strict inequalities (less than or greater than) and brackets \([]\) for inclusive inequalities (less than or equal to or greater than or equal to).
3. Since \(x\) is strictly greater than \(-2\), use a parenthesis for the left endpoint: \((-2\).
4. Since \(x\) is less than or equal to \$6\(, use a bracket for the right endpoint: \)6]$.
5. Combine these to write the interval notation as \((-2, 6]\), which represents all \(x\) values between \(-2\) and \$6\(, not including \)-2\( but including \)6$.

Key Concepts

Inequalities

Inequalities express a range of values that satisfy a condition, using symbols like <, ≤, >, and ≥. Understanding how to interpret and manipulate these symbols is essential for translating between inequality notation and interval notation.

Interval Notation

Interval notation represents sets of numbers between two endpoints, using parentheses () for exclusive bounds and brackets [] for inclusive bounds. It provides a concise way to describe solution sets of inequalities.

Relationship Between Inequalities and Interval Notation

Converting inequalities to interval notation requires recognizing whether endpoints are included or excluded based on ≤ or < symbols. For example, -2 < x ≤ 6 translates to the interval (-2, 6], where -2 is excluded and 6 is included.