Write the first five terms of the sequence whose first term is 9 and whose general term is

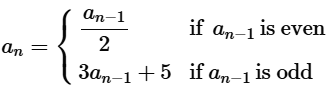
for n≥2.

Verified step by step guidance

1. Identify the first term of the sequence: \( a_1 = 9 \). This is given directly in the problem.
2. Determine the rule for finding the next term \( a_n \) based on the previous term \( a_{n-1} \): if \( a_{n-1} \) is even, then \( a_n = \frac{a_{n-1}}{2} \); if \( a_{n-1} \) is odd, then \( a_n = 3a_{n-1} + 5 \).
3. Calculate the second term \( a_2 \) by checking if \( a_1 = 9 \) is even or odd. Since 9 is odd, use the odd term formula: \( a_2 = 3 \times 9 + 5 \).
4. Calculate the third term \( a_3 \) by checking if \( a_2 \) is even or odd, then apply the corresponding formula.
5. Repeat the process for the fourth and fifth terms, each time checking the parity (even or odd) of the previous term and applying the appropriate formula to find \( a_4 \) and \( a_5 \).

Key Concepts

Sequences and Terms

A sequence is an ordered list of numbers where each number is called a term. The first term is given, and subsequent terms are found using a rule or formula. Understanding how to identify and write terms is fundamental to working with sequences.

Recursive Definition of Sequences

A recursive sequence defines each term based on the previous term(s). Here, the nth term depends on the (n-1)th term with different rules depending on whether the previous term is even or odd. Recognizing and applying recursive rules is key to generating terms.

Parity (Even and Odd Numbers)

Parity refers to whether an integer is even or odd. This property affects the rule used to find the next term in the sequence. Knowing how to determine parity helps decide which formula to apply for each term.