Which graphs in Exercises 29–34 represent functions that have ...

Question

Which graphs in Exercises 29–34 represent functions that have inverse functions?

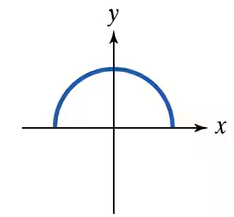
Graph of a semicircle above the x-axis centered at the origin on a coordinate plane.

Accepted Answer

Welcome back. I am so glad you're here. We are given four graphs and we're to identify which one is represented by a function and not only just being a function, but it's a function with an inverse function. Well, how do we do that? Well, we recall from previous lessons that to identify functions, we give these lines the vertical line test. And if it passes the vertical line test then to determine whether it is an inverse. If it has an inverse, we give it the horizontal line test. So let's start off with the vertical line test. You always run that one first. The vertical line test says that we're going to draw vertical lines that go up and down. And if anywhere we draw a vertical line, if we are only passing through the alleged function one time for only in this case hitting the orange line one time, then it's a function. And it passes. If we can draw one vertical line that goes through the alleged function. The orange line twice or more, then it fails the vertical line test, then it's not a function. So, let's start with a I am trying to draw a line where I go through it twice, but I can't I am only hitting it one time. So, A You are a function. Alright, let's look at B. Oh, starting right off the bat here, I am drawing a vertical line and it's running into this alleged function. This orange line twice. So this fails. Sorry B. You are not a function. You have failed the vertical line test. Let's look at C. I am trying to draw a line where I run into this orange line more than once, but I'm only hitting it once everywhere. So this is a function. Alright, see you have passed the vertical line test your function. Let's look at D. Oh no. Look draw a vertical line and I hit the orange line twice. D. You are not a function. You have failed the vertical line test. Now, let's do the horizontal line test. Horizontal lines run from left to right. Very similarly if I can draw a horizontal line and touch the alleged function line or Well in this case they're all functions. They're not alleged. But if I can touch the function line more than once, then it does not have an inverse. It fails the horizontal line test. So let's try for function A. Which is a function. Let's see if you have an inverse anywhere. I draw a horizontal line, I'm only running into our function line. One time. A You have passed the horizontal line test. You are a function with an inverse function. Let's check. See alright, where when I draw a horizontal line with function. See I am running into this multiple times. So see you do not have an inverse your function but you don't have an inverse. You fail the horizontal line test. So answer choice A. You have a function with an inverse function. Well done. We'll catch you on the next one

Which graphs in Exercises 29–34 represent functions that have inverse functions?

Key Concepts

Definition of a Function

Horizontal Line Test

Inverse Functions

Watch next