Solve each equation in Exercises 1 - 14 by factoring. 10x - 1 = (2x + 1)2
Table of contents
- 0. Review of Algebra4h 18m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations1h 43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 5m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 22m
- 10. Combinatorics & Probability1h 45m
1. Equations & Inequalities
Intro to Quadratic Equations
Problem 119
Textbook Question
Find all values of x satisfying the given conditions. y1 = 2x/(x + 2), y2 = 3/(x + 4), and y1 + y2 = 1
 Verified step by step guidance
Verified step by step guidance1
Step 1: Start by substituting the given expressions for y1 and y2 into the equation y1 + y2 = 1. This gives: \( \frac{2x}{x + 2} + \frac{3}{x + 4} = 1 \).
Step 2: To simplify the equation, find a common denominator for the fractions. The denominators are \( x + 2 \) and \( x + 4 \), so the common denominator is \( (x + 2)(x + 4) \). Rewrite each fraction with this common denominator.
Step 3: Combine the fractions into a single fraction. This results in: \( \frac{2x(x + 4) + 3(x + 2)}{(x + 2)(x + 4)} = 1 \).
Step 4: Multiply through by the common denominator \( (x + 2)(x + 4) \) to eliminate the fractions. This gives: \( 2x(x + 4) + 3(x + 2) = (x + 2)(x + 4) \).
Step 5: Expand all terms and simplify the equation. Combine like terms and rearrange the equation into standard form (e.g., \( ax^2 + bx + c = 0 \)) to solve for \( x \).
 Verified video answer for a similar problem:
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
3mPlay a video:
0 Comments
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Rational Functions
Rational functions are expressions formed by the ratio of two polynomials. In this question, y1 and y2 are rational functions where the numerator and denominator are polynomials. Understanding how to manipulate and combine these functions is essential for solving the equation y1 + y2 = 1.
Recommended video:
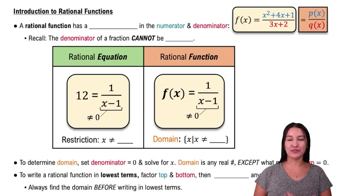
Intro to Rational Functions
Finding Common Denominators
To add or equate rational functions, it is often necessary to find a common denominator. This involves identifying the least common multiple of the denominators of the functions involved. In this case, combining y1 and y2 requires finding a common denominator to simplify the equation effectively.
Recommended video:
Guided course

Rationalizing Denominators
Solving Rational Equations
Solving rational equations involves isolating the variable, often by eliminating the denominators through multiplication. This process may introduce extraneous solutions, so it is crucial to check each solution against the original equations. In this problem, solving the equation y1 + y2 = 1 will require careful algebraic manipulation to find valid values of x.
Recommended video:

Introduction to Rational Equations

 5:35m
5:35mWatch next
Master Introduction to Quadratic Equations with a bite sized video explanation from Patrick
Start learningRelated Videos
Related Practice
Textbook Question
847
views
