Multiple Choice
A dilation maps a segment of length units to a segment of length units. What is the scale factor of the dilation?
3
views
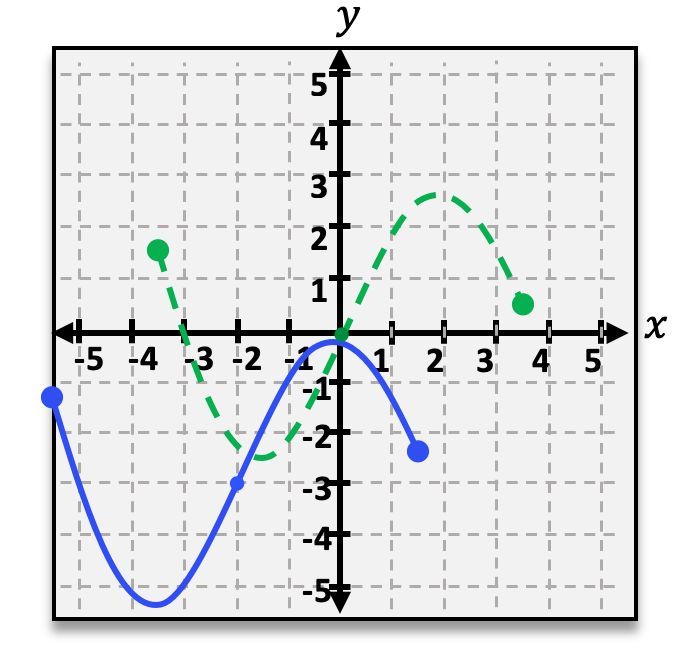
g(x)=f(x−2)+3
g(x)=f(x−2)−3
g(x)=f(x+2)−3
g(x)=f(x)−3
 Verified step by step guidance
Verified step by step guidance
 5:25m
5:25mMaster Intro to Transformations with a bite sized video explanation from Patrick
Start learning
