In Exercises 51–54, graphs of fifth-degree polynomial functions are shown. In each case, specify the number of real zeros and the number of imaginary zeros. Indicate whether there are any real zeros with multiplicity other than 1.

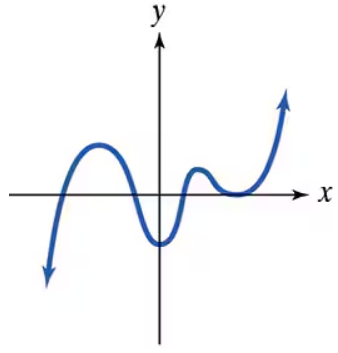
Verified step by step guidance

1. Step 1: Identify the degree of the polynomial. Since it is a fifth-degree polynomial, it has exactly 5 zeros in total (including real and imaginary zeros), according to the Fundamental Theorem of Algebra.
2. Step 2: Count the number of real zeros by observing where the graph crosses or touches the x-axis. In the graph, the polynomial crosses the x-axis at four points: approximately at x = -1, x = 1, x = 2, and one more point between 1 and 2 where the curve touches the x-axis but does not cross it.
3. Step 3: Determine the multiplicity of each real zero by analyzing the behavior of the graph at those points. If the graph crosses the x-axis, the zero has odd multiplicity (usually 1). If the graph only touches the x-axis and turns around, the zero has even multiplicity (greater than 1). Here, the zero between 1 and 2 appears to be a touch point, indicating multiplicity greater than 1.
4. Step 4: Calculate the number of imaginary zeros by subtracting the number of real zeros from the total number of zeros. Since the polynomial is degree 5 and there are 4 real zeros, the remaining zeros must be imaginary.
5. Step 5: Summarize the findings: state the number of real zeros, the number of imaginary zeros, and specify which real zeros have multiplicity greater than 1 based on the graph's behavior.

Key Concepts

Real Zeros of a Polynomial

Real zeros of a polynomial are the x-values where the graph crosses or touches the x-axis. Each zero corresponds to a root of the polynomial equation. In the graph, these are the points where the curve intersects the x-axis.

Multiplicity of Zeros

Multiplicity refers to how many times a particular zero is repeated as a root of the polynomial. If the graph touches the x-axis and turns around, the zero has even multiplicity; if it crosses the axis, the zero has odd multiplicity. Multiplicity affects the shape of the graph near the zero.

Imaginary (Complex) Zeros

Imaginary zeros are roots of the polynomial that are not real numbers and do not appear as x-intercepts on the graph. For a polynomial of degree n, the total number of zeros (real and imaginary) is n, counting multiplicities, according to the Fundamental Theorem of Algebra.