Match the rational exponent expression in Column I with the equivalent radical expression in Column II. Assume that x is not 0. ( -3x )^1/3

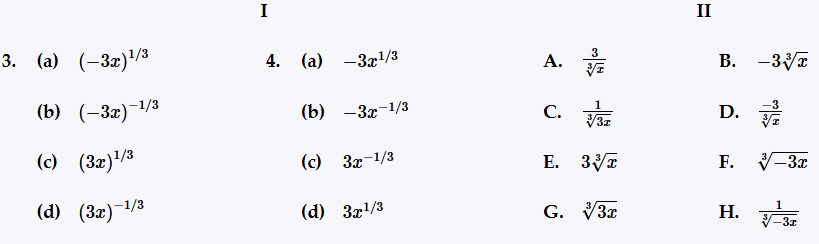
Verified step by step guidance

1. Recall that a rational exponent of the form \(a^{\frac{m}{n}}\) can be rewritten as a radical expression: \(a^{\frac{m}{n}} = \sqrt[n]{a^m}\).
2. Identify the base and the rational exponent in the expression \(( -3x )^{\frac{1}{3}}\). Here, the base is \(-3x\) and the exponent is \(\frac{1}{3}\).
3. Apply the rule for rational exponents: \(( -3x )^{\frac{1}{3}}\) is equivalent to the cube root of \(-3x\), which can be written as \(\sqrt[3]{-3x}\).
4. Understand that the cube root means finding a number which, when raised to the power of 3, gives \(-3x\).
5. Therefore, the expression \(( -3x )^{\frac{1}{3}}\) matches with the radical expression \(\sqrt[3]{-3x}\).

Key Concepts

Rational Exponents

Rational exponents express roots and powers simultaneously, where the numerator indicates the power and the denominator indicates the root. For example, x^(1/3) means the cube root of x. Understanding this allows conversion between exponential and radical forms.

Radical Expressions

Radical expressions use root symbols to represent roots of numbers or variables, such as the square root or cube root. Recognizing that x^(1/n) is equivalent to the nth root of x helps in matching expressions with rational exponents to their radical forms.

Properties of Exponents with Negative Bases

When dealing with negative bases raised to rational exponents, it is important to consider the domain and the meaning of roots. For odd roots, like cube roots, negative bases are valid, so (-3x)^(1/3) represents the cube root of -3x, preserving the negative sign inside the root.