Solve each problem. If m varies jointly as x and y, and m=10 when x=2 and y=14, find m when x=21 and y=8.
Table of contents
- 0. Review of Algebra4h 18m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations1h 43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 5m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 22m
- 10. Combinatorics & Probability1h 45m
1. Equations & Inequalities
Rational Equations
Problem 17
Textbook Question
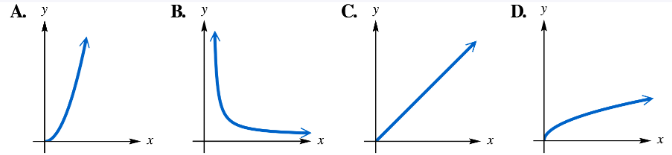
Match each statement with its corresponding graph in choices A–D. In each case, k > 0. y varies directly as x. (y=kx)
 Verified step by step guidance
Verified step by step guidance1
Understand the concept of direct variation: when we say "y varies directly as x," it means that y is proportional to x, and the relationship can be written as \(y = kx\), where \(k\) is a positive constant.
Recognize the shape of the graph for \(y = kx\) with \(k > 0\): this is a straight line passing through the origin (0,0) with a positive slope \(k\).
Identify the key features of the graph: since \(k > 0\), the line rises from left to right, meaning as \(x\) increases, \(y\) also increases proportionally.
Compare each graph choice (A–D) to these characteristics: look for the graph that is a straight line through the origin with a positive slope.
Match the statement "y varies directly as x" to the graph that fits these criteria, confirming it represents the equation \(y = kx\) with \(k > 0\).
 Verified video answer for a similar problem:
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
2mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Direct Variation
Direct variation describes a relationship where one variable is a constant multiple of another, expressed as y = kx with k > 0. This means as x increases, y increases proportionally, resulting in a straight line through the origin.
Recommended video:

Maximum Turning Points of a Polynomial Function
Slope of a Linear Function
The slope represents the rate of change of y with respect to x in a linear function. For y = kx, the slope is k, which determines the steepness and direction of the line. Since k > 0, the line rises from left to right.
Recommended video:

Linear Inequalities
Graphing Linear Equations
Graphing y = kx involves plotting points where y is proportional to x, producing a straight line through the origin (0,0). Identifying the correct graph requires recognizing this linear pattern and positive slope among the options.
Recommended video:

Categorizing Linear Equations

 5:56m
5:56mWatch next
Master Introduction to Rational Equations with a bite sized video explanation from Patrick
Start learningRelated Videos
Related Practice
Textbook Question
433
views
