Find the standard form of the equation of each hyperbola.

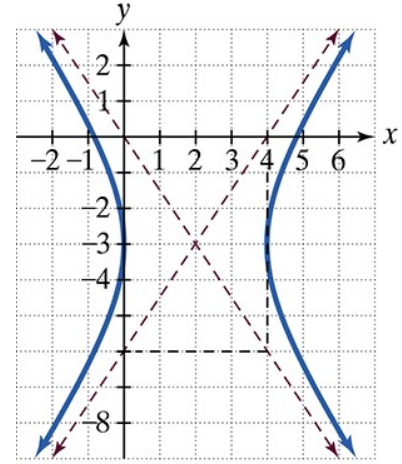
Verified step by step guidance

1. Identify the center of the hyperbola by finding the intersection point of the asymptotes. From the graph, the asymptotes intersect at the point (2, -3), so the center is (h, k) = (2, -3).
2. Determine the orientation of the hyperbola. Since the branches open left and right (horizontally), the standard form will be \( \frac{(x - h)^2}{a^2} - \frac{(y - k)^2}{b^2} = 1 \).
3. Find the slopes of the asymptotes. The asymptotes are lines passing through the center with slopes \( \pm \frac{b}{a} \). From the graph, estimate the slopes by choosing points on the asymptotes and calculating rise over run.
4. Use the slopes to find the ratio \( \frac{b}{a} \). Then, find the values of \( a \) and \( b \) by measuring the distance from the center to the vertices (which is \( a \)) and using the slope ratio to find \( b \).
5. Write the equation of the hyperbola in standard form using the center (h, k), and the values of \( a^2 \) and \( b^2 \) as \( \frac{(x - 2)^2}{a^2} - \frac{(y + 3)^2}{b^2} = 1 \).

Key Concepts

Standard Form of a Hyperbola

The standard form of a hyperbola's equation depends on its orientation and center. For a hyperbola centered at (h, k) with a horizontal transverse axis, the form is ((x - h)^2 / a^2) - ((y - k)^2 / b^2) = 1. For a vertical transverse axis, it is ((y - k)^2 / a^2) - ((x - h)^2 / b^2) = 1. Identifying the center and orientation is crucial to writing the correct equation.

Center and Transverse Axis of the Hyperbola

The center of the hyperbola is the midpoint between its vertices and the intersection of its asymptotes. The transverse axis is the line segment that passes through the vertices and determines the hyperbola's orientation (horizontal or vertical). In the graph, the center is at (2, -3), and the hyperbola opens left and right, indicating a horizontal transverse axis.

Asymptotes and Their Slopes

Asymptotes are lines that the hyperbola approaches but never touches. Their slopes help determine the values of a and b in the standard form. For a hyperbola centered at (h, k) with a horizontal transverse axis, the asymptotes have equations y - k = ±(b/a)(x - h). Using the slopes of the asymptotes from the graph allows calculation of a and b, essential for forming the equation.