Identify the 𝒚– intercept & slope of y = − 2 x − 3 y=-2x-3 y = − 2 x − 3 . Then graph the equation .

b = − 3 , m = − 2 b=-3,m=-2 b = − 3 , m = − 2

b = − 2 , m = − 3 b=-2,m=-3 b = − 2 , m = − 3

b = 2 3 , m = − 3 b=\frac23,m=-3 b = 3 2 , m = − 3

b = 2 , m = − 3 b=2,m=-3 b = 2 , m = − 3

Write the point-slope form of the equation of a line with a slope of − 2 5 -\frac25 − 5 2 that passes through (1, 3) . Then graph the equation .

y − 3 = − 2 5 ( x − 1 ) y-3=-\frac25\left(x-1\right) y − 3 = − 5 2 ( x − 1 )

y − 3 = x − 1 y-3=x-1 y − 3 = x − 1

y + 3 = 2 5 ( x + 1 ) y+3=\frac25\left(x+1\right) y + 3 = 5 2 ( x + 1 )

y = − 2 5 x − 1 y=-\frac25x-1 y = − 5 2 x − 1

Write the point-slope form of the equation of a line with a slope of 0 0 0 that passes through ( 2 , − 4 ) \left(2,-4\right) ( 2 , − 4 ) . Then graph the equation .

y + 4 = x − 2 y+4=x-2 y + 4 = x − 2

Write the point-slope form of the equation of a line that passes through the points ( 2 , 1 ) \left(2,1\right) ( 2 , 1 ) and ( − 4 , 3 ) \left(-4,3\right) ( − 4 , 3 ) . Then graph the equation .

y − 1 = − 1 3 ( x − 2 ) y-1=-\frac13\left(x-2\right) y − 1 = − 3 1 ( x − 2 )

y − 3 = − 1 3 ( x − 2 ) y-3=-\frac13\left(x-2\right) y − 3 = − 3 1 ( x − 2 )

y = 1 3 x − 4 y=\frac13x-4 y = 3 1 x − 4

y − 2 = − 1 3 ( x − 1 ) y-2=-\frac13\left(x-1\right) y − 2 = − 3 1 ( x − 1 )

Find the slope & y − i n t e r c e p t y-intercept y − in t erce pt of the line given by the equation 3 x + 2 y − 6 = 0 3x+2y-6=0 3 x + 2 y − 6 = 0

m = − 3 2 , b = 3 m=-\frac32,b=3 m = − 2 3 , b = 3

m = 2 , b = − 3 m=2,b=-3 m = 2 , b = − 3

m = 3 , b = − 3 2 m=3,b=-\frac32 m = 3 , b = − 2 3

m = 2 3 , b = 2 m=\frac23,b=2 m = 3 2 , b = 2

Write an equation of a line that passes through the point ( 3 , − 4 ) \left(3,-4\right) ( 3 , − 4 ) and is parallel to the line x + 2 y + 18 = 0 x+2y+18=0 x + 2 y + 18 = 0 .

y + 4 = − 1 2 ( x − 3 ) y+4=-\frac12\left(x-3\right) y + 4 = − 2 1 ( x − 3 )

y + 4 = − 2 ( x − 3 ) y+4=-2\left(x-3\right) y + 4 = − 2 ( x − 3 )

y = − 1 2 ( x − 3 ) y=-\frac12\left(x-3\right) y = − 2 1 ( x − 3 )

y − 3 = − 1 2 ( x + 4 ) y-3=-\frac12\left(x+4\right) y − 3 = − 2 1 ( x + 4 )

2. Graphs

Lines

2. Graphs

Lines: Videos & Practice Problems

Video Lessons Practice Worksheet

Topic summary

Understanding the slope of a line is crucial in graphing and analyzing linear equations. The slope, represented as m, is calculated using the formula $(y ₂ - y ₁) / (x ₂ - x ₁)$ , indicating the steepness of the line. Lines can be categorized as positive, negative, zero, or undefined slopes. The slope-intercept form, y = mx + b, allows for quick graphing by identifying the slope and y-intercept. Recognizing parallel and perpendicular lines is essential, as parallel lines share slopes while perpendicular lines have slopes that are negative reciprocals of each other.

concept

The Slope of a Line

Video duration:

The Slope of a Line Video Summary

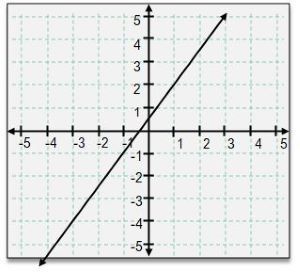
Understanding the concept of slope is essential when analyzing linear equations. The slope, denoted as m, quantifies the steepness of a line and can be calculated using any two points on that line. Mathematically, the slope is defined as the change in the y values divided by the change in the x values, expressed with the formula:

$$ m = \frac{y_2 - y_1}{x_2 - x_1} $$

In this equation, (x₁, y₁) and (x₂, y₂) represent two distinct points on the line. To simplify notation, the Greek letter delta (Δ) is often used, leading to the shorthand:

$$ m = \frac{\Delta y}{\Delta x} $$

Here, Δy represents the vertical change (rise) and Δx represents the horizontal change (run). For example, if you have two points, (1, 2) and (2, 4), you can calculate the slope as follows:

1. Identify the points: (x₁, y₁) = (1, 2) and (x₂, y₂) = (2, 4).

2. Substitute into the slope formula:

$$ m = \frac{4 - 2}{2 - 1} = \frac{2}{1} = 2 $$

This indicates that for every unit you move horizontally (run), the line rises by 2 units (rise).

When analyzing different lines, it's important to note that a steeper line will have a higher slope value. For instance, if another line has points (4, -1) and (5, 4), the slope can be calculated similarly:

1. Identify the points: (x₁, y₁) = (4, -1) and (x₂, y₂) = (5, 4).

2. Substitute into the slope formula:

$$ m = \frac{4 - (-1)}{5 - 4} = \frac{5}{1} = 5 $$

This means that for every unit you move horizontally, the line rises by 5 units, indicating a steeper incline compared to the previous line.

It’s also worth noting that the order of the points does not affect the slope calculation. For example, if you switch the points in the first example, you would still arrive at the same slope value, although the signs may change:

$$ m = \frac{2 - 4}{1 - 2} = \frac{-2}{-1} = 2 $$

In conclusion, the slope is a fundamental concept in understanding linear relationships, where a lower slope indicates a gentler incline and a higher slope indicates a steeper incline. Mastering the calculation of slope will enhance your ability to interpret and analyze linear graphs effectively.

Problem

Find the slope of the line shown below.

$m=1$

$m=\frac23$

$m=\frac32$

$m=3$

Problem

Find the slope of the line containing the points $\left(-1,1\right)$ and $\left(4,3\right)$ .

$m=\frac52$

$m=\frac25$

$m=2$

$m=\frac43$

concept

Types of Slope

Video duration:

Types of Slope Video Summary

Understanding slopes is essential in mathematics, as it describes the steepness of a line or hill. The slope is calculated using the formula:

\[ \text{slope} = \frac{\Delta y}{\Delta x} \]

where $\Delta y$ represents the change in the y-coordinate (rise) and $\Delta x$ represents the change in the x-coordinate (run). Slopes can be categorized into four types: positive, negative, zero, and undefined.

A positive slope indicates that as you move from left to right, the line rises. For example, if you select two points on a line and find that $\Delta y = 2$ and $\Delta x = 1$, the slope would be:

\[ \text{slope} = \frac{2}{1} = 2 \]

Conversely, a negative slope occurs when the line descends from left to right. If you calculate the slope for a line where $\Delta y = -1$ and $\Delta x = 1$, the slope would be:

\[ \text{slope} = \frac{-1}{1} = -1 \]

A horizontal line has a slope of zero, indicating no rise as you move along the line. For instance, if both points selected have the same y-coordinate, such as $\Delta y = 0$ and $\Delta x = 2$, the slope is:

\[ \text{slope} = \frac{0}{2} = 0 \]

In contrast, a vertical line presents a unique case where the slope is undefined. This occurs because the change in x ($\Delta x$) is zero, leading to a division by zero situation. For example, if you have $\Delta y = 3$ and $\Delta x = 0$, the slope calculation would be:

\[ \text{slope} = \frac{3}{0} \]

Since division by zero is not possible, we classify the slope of vertical lines as undefined.

Additionally, the equations of these lines follow specific forms. A horizontal line can be expressed as:

\[ y = b \]

where $b$ is a constant representing the y-value. For vertical lines, the equation takes the form:

\[ x = a \]

where $a$ is a constant representing the x-value. Understanding these concepts is crucial for analyzing linear relationships in various mathematical contexts.

Problem

Graph a line with a slope of 0 that passes through the point $\left(3,-2\right)$ .

Graphing coordinate with curve

Problem

Which of the following graphs below represents the equation $x=3$ ?

A graph of a line

concept

Slope-Intercept Form

Video duration:

Slope-Intercept Form Video Summary

Understanding the slope-intercept form of a linear equation is essential for graphing and analyzing lines. The slope-intercept form is expressed as $y = mx + b$, where $m$ represents the slope of the line and $b$ denotes the y-intercept.

The slope, $m$, can be calculated using the formula for rise over run, which is $m = \frac{\Delta y}{\Delta x}$. This means you determine how much the line rises (the change in y) for a given run (the change in x) between two points on the line. For example, if the rise is 2 and the run is 1, the slope would be 2.

The y-intercept, $b$, is the point where the line crosses the y-axis, which occurs when $x = 0$. To find the y-intercept, simply look at the graph and identify the y-coordinate at this intersection. For instance, if the graph crosses the y-axis at -3, then $b = -3$.

To construct the equation of a line in slope-intercept form, substitute the values of $m$ and $b$ into the equation. For example, if the slope is 2 and the y-intercept is 3, the equation becomes $y = 2x + 3$. If the slope is 1 and the y-intercept is -3, the equation simplifies to $y = x - 3$, as the coefficient of 1 is often omitted for simplicity.

In summary, the slope-intercept form provides a clear and concise way to express linear equations, making it easier to graph and interpret the relationships between variables.

Problem

In the graph shown, identify the y–intercept & slope. Write the equation of this line in Slope-Intercept form.

$y=\frac23x+1$

$y=-\frac23x+1$

$y=-2x+1$

$y=x+2$

concept

Graphing Lines in Slope-Intercept Form

Video duration:

Graphing Lines in Slope-Intercept Form Video Summary

To graph a line given its equation in slope-intercept form, which is expressed as y = mx + b, you can follow a straightforward three-step process. This form provides essential information: the slope (m) and the y-intercept (b). For example, consider the equation y = \frac{2}{3}x + 1.

First, identify the y-intercept and the slope. In this equation, the y-intercept (b) is 1, indicating that the line crosses the y-axis at the point (0, 1). The slope (m) is $\frac{2}{3}$, which means that for every 3 units you move to the right (run), the line rises 2 units (rise).

The second step is to plot the y-intercept on the graph. This is a simple process where you mark the point (0, 1) on the y-axis. However, a single point is not enough to define the line, so you need to find at least one more point using the slope. Starting from the y-intercept, apply the slope: from (0, 1), move up 2 units (rise) and then 3 units to the right (run) to reach the point (3, 3). Alternatively, you could move down 2 units and 3 units to the left to find another point at (-3, -1).

Finally, connect the points with a straight line. The line will extend through the points (0, 1), (3, 3), and (-3, -1), illustrating the relationship defined by the equation. This method allows you to quickly and accurately graph any linear equation in slope-intercept form.

Problem

Identify the 𝒚– intercept & slope of $y=-2x-3$ . Then graph the equation.

$b=-2,m=-3$

$b=-3,m=-2$

$b=\frac23,m=-3$

$b=2,m=-3$

concept

Point-Slope Form

Video duration:

Point-Slope Form Video Summary

In mathematics, understanding the different forms of linear equations is crucial for graphing and analyzing lines. The slope-intercept form, expressed as y = mx + b, is typically used when the slope (m) and the y-intercept (b) are known. For instance, if given the equation y = \frac{2}{3}x - 1, one can easily identify the slope as \frac{2}{3} and the y-intercept as -1, allowing for straightforward graphing by plotting the y-intercept and using the slope to find additional points.

However, there are situations where you may only know the slope and a specific point through which the line passes. In such cases, the point-slope form of a linear equation is more appropriate. This form is represented as y - y_1 = m(x - x_1), where (x_1, y_1) is a point on the line. For example, if a line has a slope of \frac{2}{3} and passes through the point (3, 1), you can substitute these values into the point-slope equation. This results in y - 1 = \frac{2}{3}(x - 3), effectively capturing the relationship between the slope and the specific point.

To graph the line using the point-slope form, start at the point (3, 1). From there, apply the slope of \frac{2}{3} by moving up 2 units and right 3 units to find another point on the line. Alternatively, you can move down 2 units and left 3 units to find a point in the opposite direction. Connecting these points will yield the graph of the line.

To further illustrate the equivalence of the two forms, one can convert the point-slope equation back to slope-intercept form. Starting from y - 1 = \frac{2}{3}(x - 3), distribute the slope to obtain y - 1 = \frac{2}{3}x - 2. Adding 1 to both sides results in y = \frac{2}{3}x - 1, which matches the original slope-intercept form. This demonstrates that both forms represent the same line, just expressed differently.

In summary, the slope-intercept form is ideal when the slope and y-intercept are known, while the point-slope form is useful when given a slope and a specific point. Understanding how to transition between these forms enhances your ability to work with linear equations effectively.

Problem

Write the point-slope form of the equation of a line with a slope of $-\frac25$ that passes through (1, 3). Then graph the equation.

$y-3=-\frac25\left(x-1\right)$

$y-3=x-1$

$y+3=\frac25\left(x+1\right)$

$y=-\frac25x-1$

Problem

Write the point-slope form of the equation of a line with a slope of $0$ that passes through $\left(2,-4\right)$ . Then graph the equation.

$y+4=x-2$

$y+4=x$

$y+4=0$

$y=0$

concept

Finding Equations of Lines Given Two Points

Video duration:

Finding Equations of Lines Given Two Points Video Summary

When working with linear equations, particularly in point-slope form, it's essential to understand how to derive the slope when only two points are provided. The point-slope form of a linear equation is expressed as:

y - y₁ = m(x - x₁)

In this equation, m represents the slope, while (x₁, y₁) is a specific point on the line. If the slope is not given, it can be calculated using the coordinates of the two points. For two points (x₁, y₁) and (x₂, y₂), the slope m can be determined using the formula:

m = \frac{y₂ - y₁}{x₂ - x₁}

For example, if the points are (-1, -5) and (2, 4), we can assign:

x₁ = -1, y₁ = -5
x₂ = 2, y₂ = 4

Substituting these values into the slope formula gives:

m = \frac{4 - (-5)}{2 - (-1)} = \frac{4 + 5}{2 + 1} = \frac{9}{3} = 3

Now that we have the slope, we can substitute m back into the point-slope form. Using the point (-1, -5), the equation becomes:

y - (-5) = 3(x - (-1))

This simplifies to:

y + 5 = 3(x + 1)

This equation represents the line that passes through the two given points. To graph this line, plot the points (-1, -5) and (2, 4) on a coordinate plane and draw a straight line connecting them. This method illustrates that regardless of which point is chosen as (x₁, y₁), the resulting equation will remain consistent, confirming the reliability of the point-slope form in linear equations.

Problem

Write the point-slope form of the equation of a line that passes through the points $\left(2,1\right)$ and $\left(-4,3\right)$ . Then graph the equation.

$y-1=-\frac13\left(x-2\right)$

$y-3=-\frac13\left(x-2\right)$

$y=\frac13x-4$

$y-2=-\frac13\left(x-1\right)$

concept

Standard Form of Line Equations

Video duration:

Standard Form of Line Equations Video Summary

In mathematics, understanding the different forms of linear equations is crucial for solving problems effectively. One such form is the standard form of a linear equation, which is typically expressed as Ax + By + C = 0. This format allows for a clear representation of the relationship between the variables x and y, where A, B, and C are constants. While it may seem unfamiliar compared to the more commonly used slope-intercept form y = mx + b, both forms convey the same information about a line.

To convert an equation from standard form to slope-intercept form, the goal is to isolate y on one side of the equation. For example, consider the equation -9x + 3y - 120 = 0. To rewrite this in slope-intercept form, you would first rearrange the equation to isolate y:

3y = 9x + 120

Next, divide every term by 3 to solve for y:

y = 3x + 40

From this equation, it is clear that the slope (m) is 3 and the y-intercept (b) is 40. This process illustrates how different forms of the same equation can provide valuable insights into the line's characteristics.

Additionally, the standard form is particularly useful for quickly finding the x and y intercepts of a line without converting to slope-intercept form. The x-intercept occurs where y equals 0, while the y-intercept occurs where x equals 0. For instance, given the standard form equation 3x + 2y - 6 = 0, you can find the x-intercept by setting y to 0:

3x - 6 = 0 leads to x = 2.

For the y-intercept, set x to 0:

2y - 6 = 0 leads to y = 3.

Thus, the intercepts are (2, 0) and (0, 3), which can be plotted to graph the line. Connecting these two points provides a visual representation of the linear equation.

In summary, mastering the conversion between standard form and slope-intercept form, as well as understanding how to find intercepts directly from standard form, enhances your ability to analyze and graph linear equations effectively.

Problem

Find the slope & $y-intercept$ of the line given by the equation $3x+2y-6=0$

$m=2,b=-3$

$m=-\frac32,b=3$

$m=3,b=-\frac32$

$m=\frac23,b=2$

Problem

Graph the equation $9x+6y+18=0$ by finding the intercepts.

A graph with a line

concept

Parallel & Perpendicular Lines

Video duration:

Parallel & Perpendicular Lines Video Summary

Understanding the relationship between parallel and perpendicular lines is essential in geometry, particularly when working with linear equations. Parallel lines are characterized by having the same slope but different y-intercepts. For instance, if we consider the equations of two lines, such as y = -3x + 2 and y = -3x - 4, both lines have a slope of -3, indicating they are parallel. This means they will never intersect, as their rise over run remains constant, despite their different y-intercepts (2 and -4).

On the other hand, perpendicular lines intersect at right angles (90 degrees). The slopes of perpendicular lines are related in a specific way: they are negative reciprocals of each other. For example, if one line has a slope of -3, a line perpendicular to it would have a slope of $\frac{1}{3}$. This relationship ensures that the product of their slopes equals -1, confirming their perpendicularity.

When tasked with writing the equation of a line parallel to a given line, one must maintain the same slope while altering the y-intercept. For example, to find a line parallel to y = 2x - 6 that passes through the point (-1, 4), we use the point-slope form of the equation: y - y_1 = m(x - x_1). Here, m = 2 (the slope) and the point (-1, 4) gives us y - 4 = 2(x + 1), which simplifies to y = 2x + 6.

Conversely, when finding a line that is perpendicular to a given line, one must first determine the slope of the original line and then find its negative reciprocal. For instance, if we have a line in standard form and we convert it to slope-intercept form to find its slope, we can then calculate the perpendicular slope. If the original line has a slope of -1/4, the perpendicular slope would be 4. Given a y-intercept of 3, the equation of the perpendicular line can be expressed as y = 4x + 3.

In summary, recognizing the characteristics of parallel and perpendicular lines allows for the effective manipulation of linear equations. By understanding slopes and y-intercepts, one can easily derive new equations that maintain the desired relationships between lines.

Problem

Write an equation of a line that passes through the point $\left(3,-4\right)$ and is parallel to the line $x+2y+18=0$ .

$y+4=-\frac12\left(x-3\right)$

$y+4=-2\left(x-3\right)$

$y=-\frac12\left(x-3\right)$

$y-3=-\frac12\left(x+4\right)$

Do you want more practice?

Go over this topic definitions with flashcards

More sets

Lines definitions
2. Graphs
15 Terms

Here’s what students ask on this topic:

What is the slope of a line and how is it calculated?

The slope of a line, represented by the variable $m$ , measures the steepness or incline of the line. It is calculated using the formula $\frac{y_{2} - y_{1}}{x_{2} - x_{1}}$ , where $y_{2}$ and $y_{1}$ are the y-coordinates of two points on the line, and $x_{2}$ and $x_{1}$ are the x-coordinates of those points. This formula essentially measures the change in the y-values (rise) divided by the change in the x-values (run). A positive slope indicates the line rises as it moves from left to right, while a negative slope indicates it falls.

Created using AI

What are the different types of slopes a line can have?

A line can have four types of slopes: positive, negative, zero, and undefined. A positive slope means the line rises from left to right, indicating an upward trend. A negative slope means the line falls from left to right, indicating a downward trend. A zero slope means the line is horizontal, indicating no vertical change as it moves along the x-axis. An undefined slope occurs when the line is vertical, meaning there is no horizontal change, and the denominator in the slope formula is zero, which makes the slope undefined.

Created using AI

How do you write the equation of a line in slope-intercept form?

The slope-intercept form of a line's equation is $y = m x + b$ , where $m$ represents the slope and $b$ represents the y-intercept, the point where the line crosses the y-axis. To write the equation, you need to determine the slope $m$ and the y-intercept $b$ . For example, if a line has a slope of 2 and crosses the y-axis at 3, the equation would be $y = 2 x + 3$ .

Created using AI

What is the difference between parallel and perpendicular lines?

Parallel lines have the same slope but different y-intercepts, meaning they never intersect and are always the same distance apart. For example, the lines $y = 2 x + 3$ and $y = 2 x - 4$ are parallel. Perpendicular lines intersect at a right angle (90 degrees). Their slopes are negative reciprocals of each other. For example, if one line has a slope of $2$ , a line perpendicular to it will have a slope of $- \frac{1}{2}$ .

Created using AI

How do you graph a line given its equation in slope-intercept form?

To graph a line given its equation in slope-intercept form $y = m x + b$ , follow these steps: First, plot the y-intercept $b$ on the y-axis. This is the point where the line crosses the y-axis. Next, use the slope $m$ to determine the rise over run from the y-intercept. For example, if the slope is $2$ , move up 2 units and 1 unit to the right to plot the next point. Finally, draw a straight line through these points to complete the graph.

Created using AI

Your Precalculus tutors

Patrick Ford

Physics and Math Lead Instructor

Lines: Videos & Practice Problems

The Slope of a Line

The Slope of a Line Video Summary

Find the slope of the line shown below.

Find the slope of the line containing the points (−1,1)\left(-1,1\right)(−1,1) and (4,3)\left(4,3\right)(4,3).

Types of Slope

Types of Slope Video Summary

Graph a line with a slope of 0 that passes through the point (3,−2)\left(3,-2\right)(3,−2).

Which of the following graphs below represents the equation x=3x=3x=3?

Slope-Intercept Form

Slope-Intercept Form Video Summary

In the graph shown, identify the y–intercept & slope. Write the equation of this line in Slope-Intercept form.

Graphing Lines in Slope-Intercept Form

Graphing Lines in Slope-Intercept Form Video Summary

Identify the 𝒚– intercept & slope of y=−2x−3y=-2x-3y=−2x−3 . Then graph the equation.

Point-Slope Form

Point-Slope Form Video Summary

Write the point-slope form of the equation of a line with a slope of −25-\frac25−52 that passes through (1, 3). Then graph the equation.

Write the point-slope form of the equation of a line with a slope of 000 that passes through (2,−4)\left(2,-4\right)(2,−4) . Then graph the equation.

Finding Equations of Lines Given Two Points

Finding Equations of Lines Given Two Points Video Summary

Write the point-slope form of the equation of a line that passes through the points (2,1)\left(2,1\right)(2,1) and (−4,3)\left(-4,3\right)(−4,3) . Then graph the equation.

Standard Form of Line Equations

Standard Form of Line Equations Video Summary

Find the slope & y−intercepty-intercepty−intercept of the line given by the equation 3x+2y−6=03x+2y-6=03x+2y−6=0

Graph the equation 9x+6y+18=09x+6y+18=09x+6y+18=0 by finding the intercepts.

Parallel & Perpendicular Lines

Parallel & Perpendicular Lines Video Summary

Write an equation of a line that passes through the point (3,−4)\left(3,-4\right)(3,−4) and is parallel to the line x+2y+18=0x+2y+18=0x+2y+18=0.

Do you want more practice?

Go over this topic definitions with flashcards

Here’s what students ask on this topic:

What is the slope of a line and how is it calculated?

What are the different types of slopes a line can have?

How do you write the equation of a line in slope-intercept form?

What is the difference between parallel and perpendicular lines?

How do you graph a line given its equation in slope-intercept form?

Your Precalculus tutors

Find the slope of the line containing the points $\left(-1,1\right)$ and $\left(4,3\right)$ .

Graph a line with a slope of 0 that passes through the point $\left(3,-2\right)$ .

Which of the following graphs below represents the equation $x=3$ ?

Identify the 𝒚– intercept & slope of $y=-2x-3$ . Then graph the equation.

Write the point-slope form of the equation of a line with a slope of $-\frac25$ that passes through (1, 3). Then graph the equation.

Write the point-slope form of the equation of a line with a slope of $0$ that passes through $\left(2,-4\right)$ . Then graph the equation.

Write the point-slope form of the equation of a line that passes through the points $\left(2,1\right)$ and $\left(-4,3\right)$ . Then graph the equation.

Find the slope & $y-intercept$ of the line given by the equation $3x+2y-6=0$

Graph the equation $9x+6y+18=0$ by finding the intercepts.

Write an equation of a line that passes through the point $\left(3,-4\right)$ and is parallel to the line $x+2y+18=0$ .