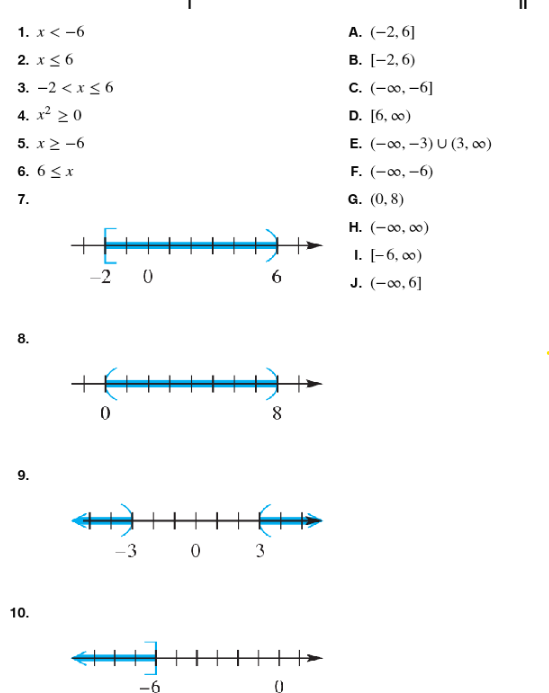
Match the inequality in each exercise in Column I with its equivalent interval notation in Column II. x²≥0

Verified step by step guidance

1. Recognize that the inequality given is \(x^2 \geq 0\). This means we are looking for all values of \(x\) such that the square of \(x\) is greater than or equal to zero.
2. Recall that the square of any real number is always non-negative, so \(x^2 \geq 0\) is true for every real number \(x\).
3. Therefore, the solution set includes all real numbers, which in interval notation is expressed as \((-\infty, \infty)\).
4. Match the inequality \(x^2 \geq 0\) from Column I with the interval notation \((-\infty, \infty)\) from Column II.
5. Confirm that this interval notation correctly represents the solution set of the inequality, meaning all real numbers satisfy the inequality.

Key Concepts

Inequalities and Their Solutions

An inequality compares two expressions using symbols like ≥, ≤, >, or <. Solving an inequality involves finding all values of the variable that make the inequality true. For example, x² ≥ 0 means finding all x such that the square of x is nonnegative.

Properties of Squares of Real Numbers

The square of any real number x, denoted x², is always greater than or equal to zero. This property implies that x² ≥ 0 holds for all real numbers x, which is important when translating inequalities involving squares into interval notation.

Interval Notation

Interval notation is a way to represent sets of numbers between two endpoints. It uses brackets [ ] for inclusive boundaries and parentheses ( ) for exclusive boundaries. For example, the solution to x² ≥ 0 is all real numbers, represented as (-∞, ∞) in interval notation.