Write an equation involving absolute value that says the distance between p and q is 2 units.
Table of contents
- 0. Review of Algebra4h 18m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations1h 43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 5m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 22m
- 10. Combinatorics & Probability1h 45m
2. Graphs of Equations
Graphs and Coordinates
Problem 18
Textbook Question
Use the graph to determine (a) the function's domain, (b) the function's range, (c) the x-intercepts, if any, (d) the y-intercept, if there is one, (e) intervals on which the function is increasing, decreasing or constant, (f) the missing function values, indicated by question marks, below each graph.

 Verified step by step guidance
Verified step by step guidance1
Step 1: To determine the domain of the function, observe the graph horizontally along the x-axis. The graph extends indefinitely to the left and right, meaning the domain is all real numbers, expressed as (-∞, ∞).
Step 2: To find the range of the function, observe the graph vertically along the y-axis. The lowest point of the graph is at y = -3, and the graph increases indefinitely upwards. Therefore, the range is [-3, ∞).
Step 3: To identify the x-intercepts, locate the points where the graph crosses the x-axis. From the graph, the x-intercepts are at x = -2 and x = 2.
Step 4: To find the y-intercept, locate the point where the graph crosses the y-axis. From the graph, the y-intercept is at y = -3.
Step 5: To determine intervals of increase and decrease, observe the slope of the graph. The function decreases on the interval (-∞, 0) and increases on the interval (0, ∞).
 Verified video answer for a similar problem:
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
1mPlay a video:
0 Comments
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Domain
The domain of a function refers to the set of all possible input values (x-values) for which the function is defined. In the context of a graph, the domain can be determined by identifying the horizontal extent of the graph. For a quadratic function, the domain is typically all real numbers unless specified otherwise.
Recommended video:
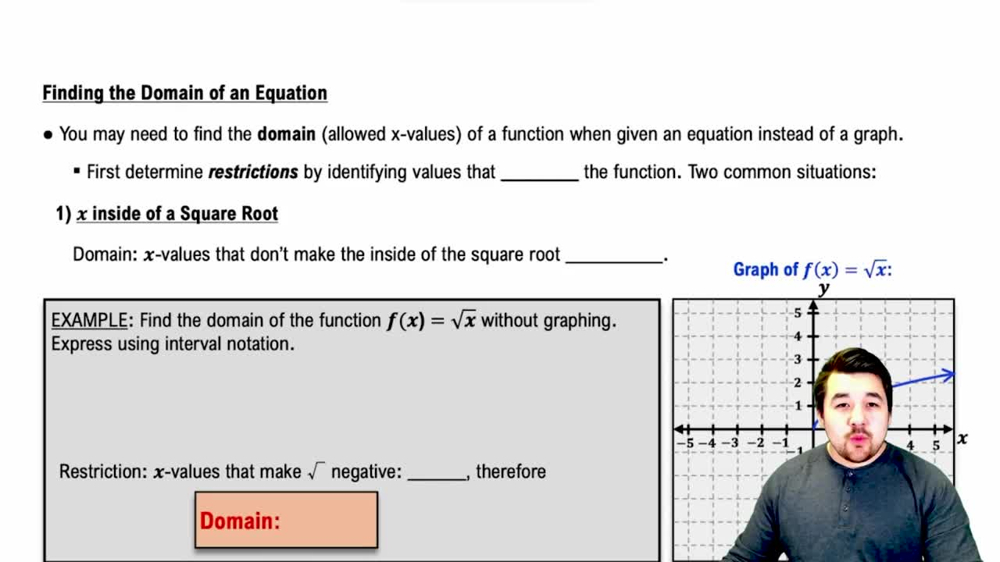
Finding the Domain of an Equation
Range
The range of a function is the set of all possible output values (y-values) that the function can produce. For a quadratic function, the range can be found by looking at the vertical extent of the graph. The vertex of the parabola indicates the minimum or maximum value, which helps define the range based on whether the parabola opens upwards or downwards.
Recommended video:
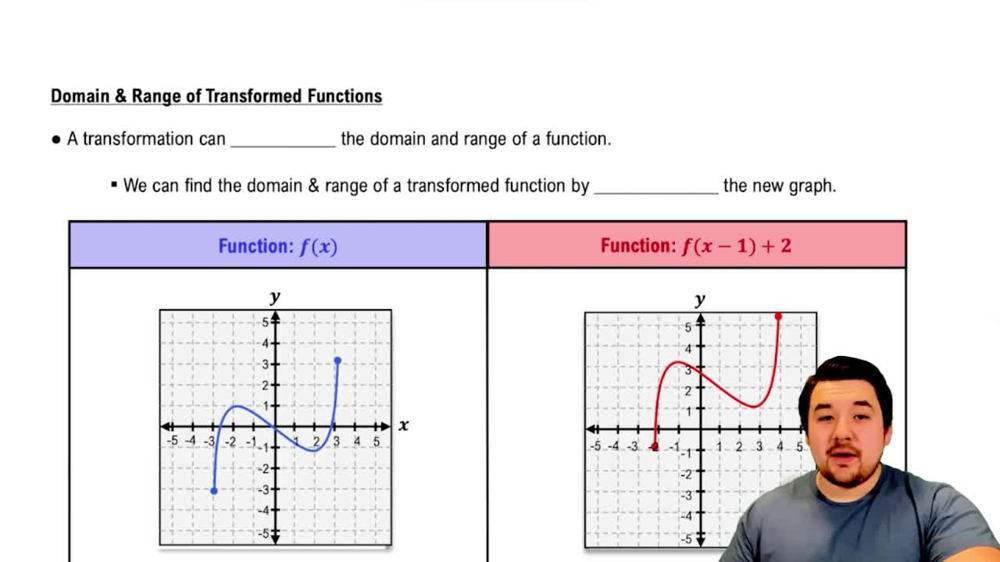
Domain & Range of Transformed Functions
Intercepts
Intercepts are points where the graph of a function crosses the axes. The x-intercepts occur where the function's output is zero (y=0), while the y-intercept occurs where the input is zero (x=0). Identifying these points is crucial for understanding the behavior of the function and can be visually determined from the graph.
Recommended video:
Guided course
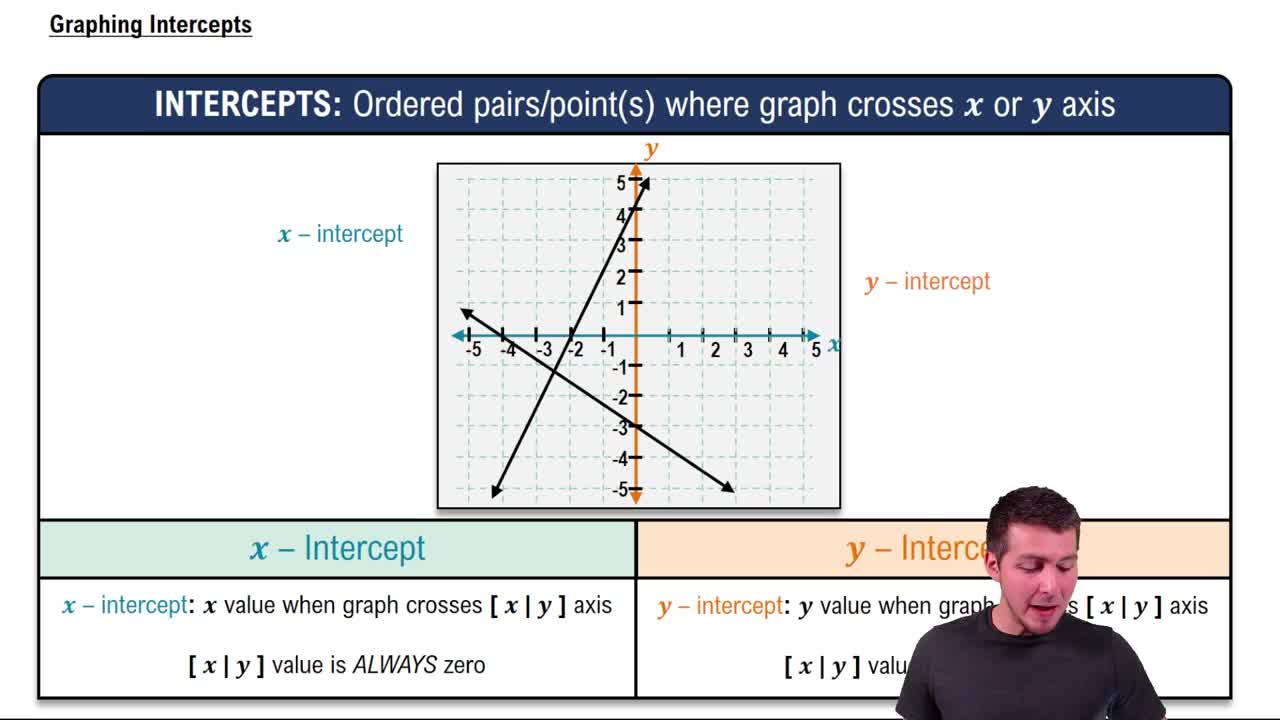
Graphing Intercepts
Related Videos
Related Practice
Textbook Question
516
views


