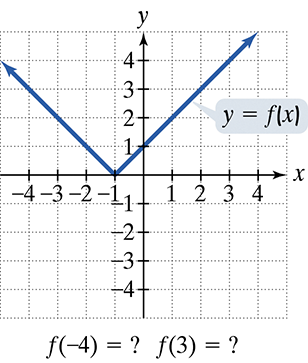
In Exercises 77–92, use the graph to determine a. the function's domain; b.the x-intercepts, if any; and e. the missing function values, indicated by question marks, below each graph.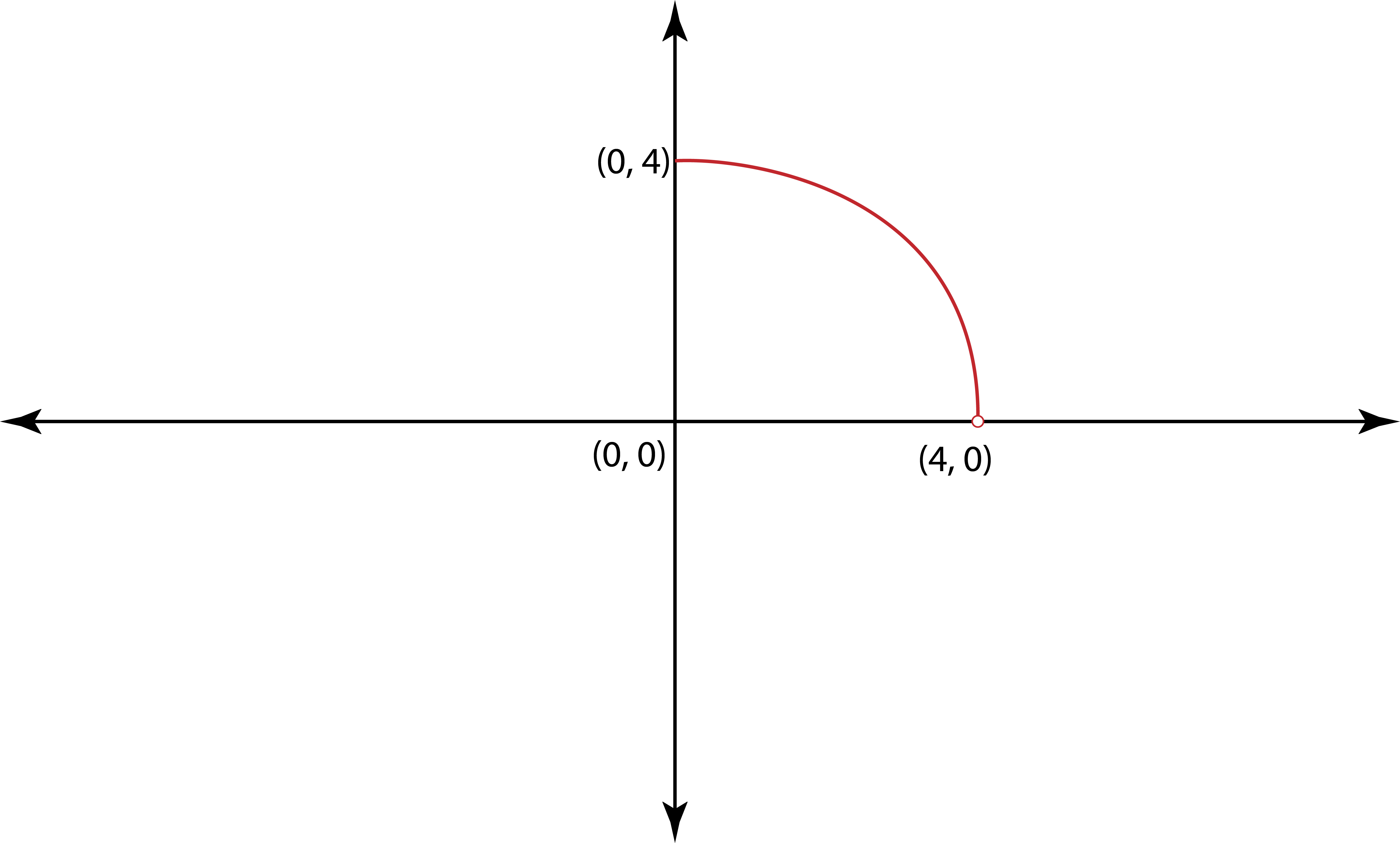

Verified step by step guidance

1. Step 1: To determine the domain of the function, observe the x-values for which the function is defined. For the first graph, the function is defined from x = 0 to x = 4. For the second graph, the function is defined for all x-values.
2. Step 2: To find the x-intercepts, look for the points where the graph crosses the x-axis. For the first graph, the x-intercept is at (4, 0). For the second graph, the x-intercept is at (0, 0).
3. Step 3: To find the missing function values, locate the corresponding y-values for the given x-values on the graph. For the second graph, find the y-values for x = -4 and x = 3.
4. Step 4: For the second graph, when x = -4, trace vertically to the graph to find the y-value. Similarly, when x = 3, trace vertically to the graph to find the y-value.
5. Step 5: Summarize the findings: The domain, x-intercepts, and missing function values for each graph.

Key Concepts

Domain of a Function

The domain of a function refers to the set of all possible input values (x-values) for which the function is defined. Understanding the domain is crucial for determining where the function can be evaluated, which can be influenced by factors such as discontinuities or restrictions in the function's definition.

X-Intercepts

X-intercepts are the points where a function crosses the x-axis, meaning the output value (y) is zero at these points. To find x-intercepts, one typically sets the function equal to zero and solves for x. Identifying these points is essential for understanding the behavior of the function and its graphical representation.

Function Values

Function values represent the output of a function for given input values. In the context of a graph, these values can be determined by evaluating the function at specific x-values. Missing function values, often indicated by question marks, require careful analysis of the graph to estimate or calculate the corresponding y-values.