Graph each linear function. 6x-5f(x) - 20 = 0
Table of contents
- 0. Review of Algebra4h 18m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations1h 43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 5m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 22m
- 10. Combinatorics & Probability1h 45m
2. Graphs of Equations
Lines
Problem 19
Textbook Question
Write an equation in slope-intercept form of a linear function f whose graph satisfies the given conditions. The graph of ƒ passes through (−1, 5) and is perpendicular to the line whose equation is x = 6.
 Verified step by step guidance
Verified step by step guidance1
Identify the slope of the given line. The line given is \( x = 6 \), which is a vertical line. Vertical lines have an undefined slope.
Determine the slope of the line perpendicular to the given line. Since the given line is vertical, the perpendicular line must be horizontal, which means its slope is \( 0 \).
Use the point-slope form of a line equation with the slope \( m = 0 \) and the point \( (-1, 5) \). The point-slope form is \( y - y_1 = m(x - x_1) \).
Substitute the values into the point-slope form: \( y - 5 = 0 \times (x + 1) \). Simplify the right side to get \( y - 5 = 0 \).
Solve for \( y \) to write the equation in slope-intercept form \( y = mx + b \). This gives \( y = 5 \), which is the equation of the line perpendicular to \( x = 6 \) passing through \( (-1, 5) \).
 Verified video answer for a similar problem:
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
2mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Slope-Intercept Form
The slope-intercept form of a linear equation is y = mx + b, where m represents the slope and b is the y-intercept. This form makes it easy to identify the slope and where the line crosses the y-axis, which is essential for graphing and writing linear equations.
Recommended video:
Guided course
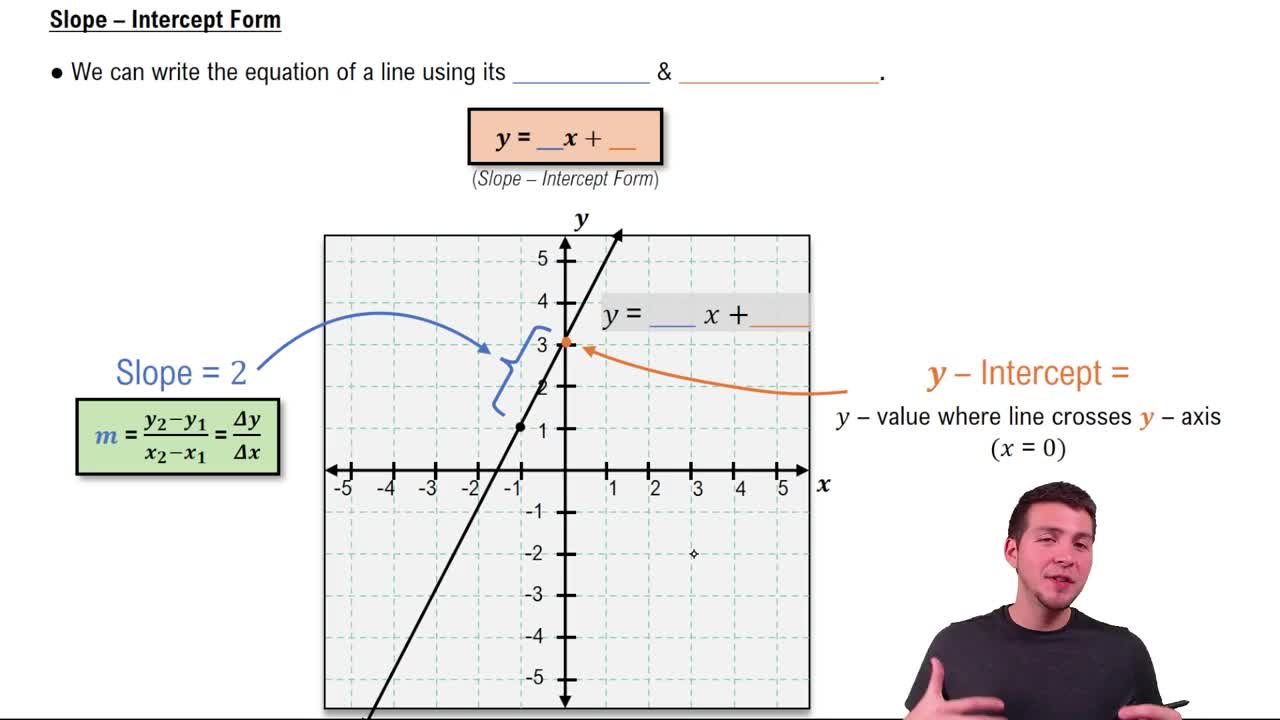
Slope-Intercept Form
Perpendicular Lines
Two lines are perpendicular if their slopes are negative reciprocals of each other. For vertical and horizontal lines, a vertical line has an undefined slope, and a line perpendicular to it is horizontal with a slope of zero. Understanding this helps determine the slope of the required line.
Recommended video:
Guided course

Parallel & Perpendicular Lines
Using a Point to Find the Equation
Given a point on the line and the slope, you can substitute these values into the slope-intercept form to solve for the y-intercept b. This step is crucial to write the specific equation of the line that meets the given conditions.
Recommended video:
Guided course

Finding Equations of Lines Given Two Points
Related Videos
Related Practice
Textbook Question
44
views


