Use the given conditions to write an equation for each line in point-slope form and slope-intercept form. Passing through (−3, 6) and (3, −2)
Table of contents
- 0. Review of Algebra4h 18m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations1h 43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 5m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 22m
- 10. Combinatorics & Probability1h 45m
2. Graphs of Equations
Lines
Problem 63
Textbook Question
In Exercises 59-66, a. Rewrite the given equation in slope-intercept form. b. Give the slope and y-intercept. c. Use the slope and y-intercept to graph the linear function. 8x – 4y – 12 =0
 Verified step by step guidance
Verified step by step guidance1
Start by rewriting the given equation \$8x - 4y - 12 = 0\( in slope-intercept form, which is \)y = mx + b\(, where \)m\( is the slope and \)b$ is the y-intercept.
Isolate the \(y\) term on one side. Add \$4y\( to both sides and subtract \)12\( from both sides to get \)8x - 12 = 4y$.
Divide every term by 4 to solve for \(y\): \(\frac{8x}{4} - \frac{12}{4} = y\), which simplifies to \(y = 2x - 3\).
Identify the slope \(m\) and y-intercept \(b\) from the equation \(y = 2x - 3\). Here, the slope \(m\) is 2, and the y-intercept \(b\) is \(-3\).
To graph the function, start by plotting the y-intercept at \((0, -3)\) on the coordinate plane. Then use the slope \$2$ (which means rise over run = 2/1) to find another point by moving up 2 units and right 1 unit from the y-intercept, and draw the line through these points.
 Verified video answer for a similar problem:
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
5mPlay a video:
0 Comments
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
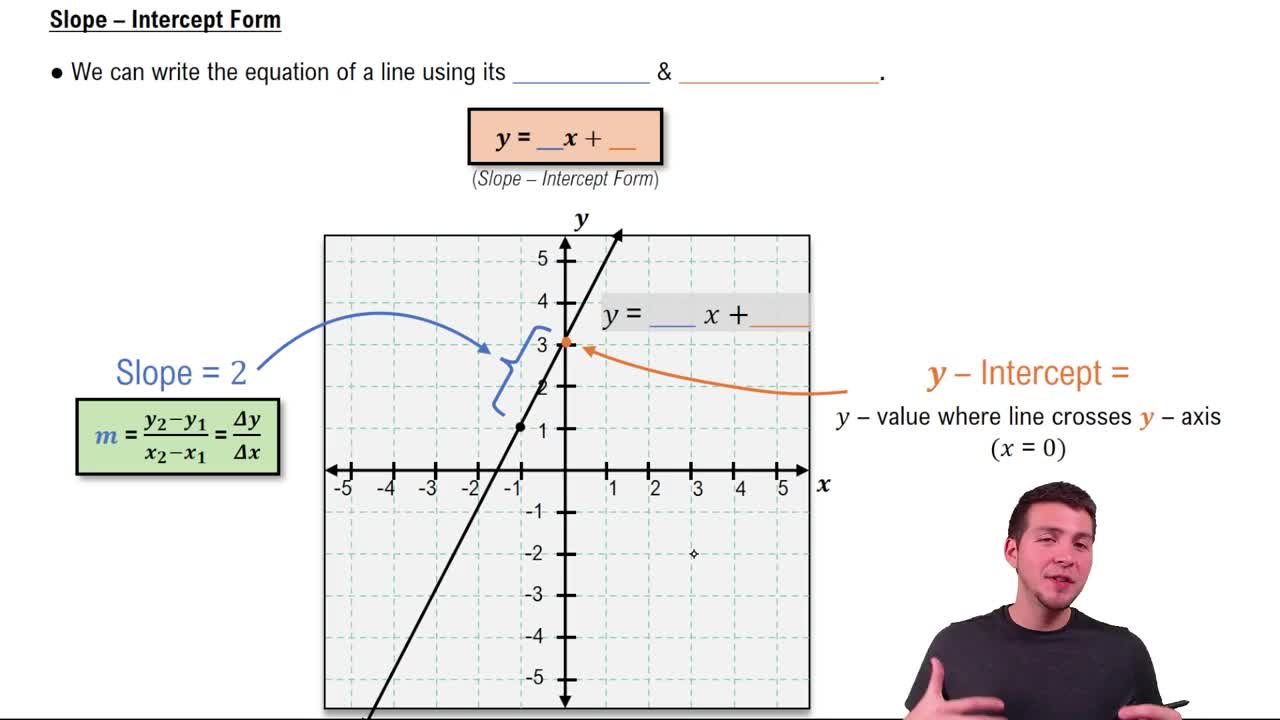
Slope-Intercept Form
The slope-intercept form of a linear equation is y = mx + b, where m represents the slope and b represents the y-intercept. Rewriting an equation into this form makes it easier to identify these values and to graph the line.
Recommended video:
Guided course
Slope-Intercept Form
Slope of a Line
The slope (m) measures the steepness and direction of a line, calculated as the ratio of the change in y to the change in x (rise over run). It indicates how much y changes for a unit change in x and is essential for understanding the line's behavior.
Recommended video:
Guided course

The Slope of a Line
Graphing Using Slope and Y-Intercept
Graphing a linear function involves plotting the y-intercept (where the line crosses the y-axis) and then using the slope to find other points by moving vertically and horizontally. This method provides a straightforward way to visualize the line on the coordinate plane.
Recommended video:
Guided course

Graphing Lines in Slope-Intercept Form
Related Videos
Related Practice
Textbook Question
94
views


