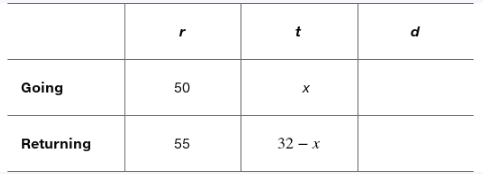
Solve each problem. See Example 2. Elwyn averaged 50 mph traveling from Denver to Minneapolis. Returning by a different route that covered the same number of miles, he averaged 55 mph. What is the distance between the two cities to the nearest ten miles if his total traveling time was 32 hr?

Verified step by step guidance

1. Let the distance between Denver and Minneapolis be \(d\) miles. Since the return trip covers the same distance, both trips are \(d\) miles each.
2. Write expressions for the time taken for each leg of the trip using the formula \(\text{time} = \frac{\text{distance}}{\text{speed}}\). For the trip to Minneapolis, time is \(\frac{d}{50}\) hours, and for the return trip, time is \(\frac{d}{55}\) hours.
3. Set up an equation for the total travel time by adding the two times and equating to 32 hours: \(\frac{d}{50} + \frac{d}{55} = 32\).
4. Find a common denominator for the fractions on the left side, which is \(50 \times 55 = 2750\), and rewrite the equation as \(\frac{55d}{2750} + \frac{50d}{2750} = 32\).
5. Combine the fractions to get \(\frac{105d}{2750} = 32\), then solve for \(d\) by multiplying both sides by 2750 and dividing by 105: \(d = \frac{32 \times 2750}{105}\). This will give the distance between the two cities.

Key Concepts

Distance-Speed-Time Relationship

This fundamental concept relates distance, speed, and time through the formula distance = speed × time. Understanding how to manipulate this formula is essential for solving problems involving travel, as it allows you to express one variable in terms of the others.

Average Speed and Different Routes

When traveling the same distance at different speeds, the total time is the sum of individual times for each leg. Recognizing that the distance is constant but speeds vary helps set up equations to find unknown distances or times.

Setting Up and Solving Algebraic Equations

Translating the word problem into algebraic expressions and equations is crucial. Here, expressing total time as the sum of times for each leg and solving for distance requires forming and solving a rational equation.