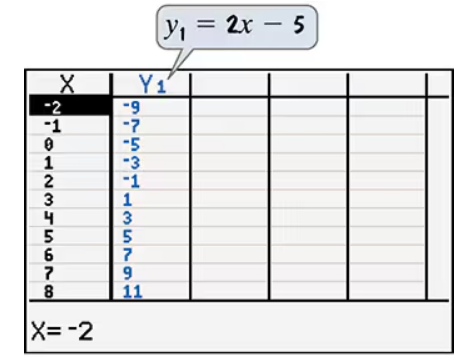
Use the table to solve each inequality. - 3 < 2x - 5 ≤ 3

Verified step by step guidance

1. Start with the compound inequality: \$3 < 2x - 5 \leq 3$.
2. Break the compound inequality into two separate inequalities: 1) \$3 < 2x - 5$ 2) \$2x - 5 \leq 3$.
3. Solve the first inequality \$3 < 2x - 5\( by adding 5 to both sides: \)3 + 5 < 2x\(, which simplifies to \)8 < 2x\(. Then divide both sides by 2 to isolate \)x\(: \)4 < x$.
4. Solve the second inequality \$2x - 5 \leq 3\( by adding 5 to both sides: \)2x \leq 8\(. Then divide both sides by 2: \)x \leq 4$.
5. Combine the two results to find the solution to the compound inequality: \$4 < x \leq 4\(. Since this is a contradiction (no number is both greater than 4 and less than or equal to 4), check the table values for \)x\( and \)y = 2x - 13\( to verify if any \)x$ satisfies the original inequality.

Key Concepts

Solving Compound Inequalities

A compound inequality involves two inequalities joined by 'and' or 'or'. To solve, treat each inequality separately and find the intersection (for 'and') or union (for 'or') of their solution sets. For example, solving 3 < 2x - 5 ≤ 3 requires isolating x in both inequalities and combining the results.

Using Tables to Solve Inequalities

Tables can help solve inequalities by providing values of expressions for specific x-values. By comparing the expression values to the inequality bounds, you can identify which x-values satisfy the inequality. This method is useful when direct algebraic manipulation is complex or when verifying solutions.

Linear Functions and Their Graphs

A linear function like y = 2x - 13 produces a straight line when graphed. Understanding how changes in x affect y helps solve inequalities involving linear expressions. The table shows corresponding y-values for given x-values, illustrating the function's behavior and aiding in solving inequalities.