An objective function and a system of linear inequalities representing constraints are given. a. Graph the system of inequalities representing the constraints. b. Find the value of the objective function at each corner of the graphed region. c. Use the values in part (b) to determine the maximum value of the objective function and the values of x and y for which the maximum occurs.
Table of contents
- 0. Review of Algebra4h 18m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations1h 43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 5m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 22m
- 10. Combinatorics & Probability1h 45m
7. Systems of Equations & Matrices
Graphing Systems of Inequalities
Multiple Choice
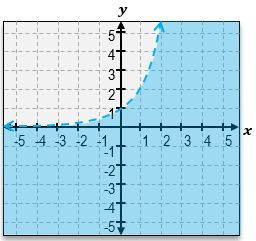
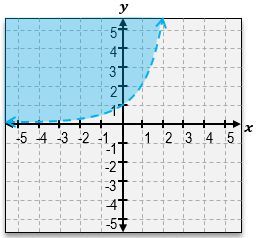
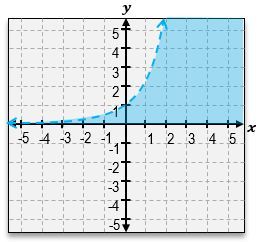
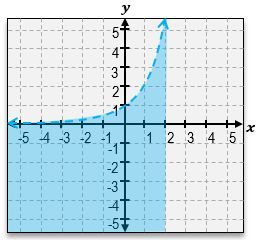
Graph the inequality y < 2x.
A
B
C
D
0 Comments
 Verified step by step guidance
Verified step by step guidance1
Identify the inequality to be graphed: y < 2^x.
Graph the boundary line y = 2^x. Since the inequality is '<', use a dashed line to indicate that points on the line are not included in the solution.
Determine which side of the boundary line to shade. Choose a test point not on the line, such as (0,0), and substitute it into the inequality.
If the test point satisfies the inequality, shade the region containing the test point. If not, shade the opposite region.
The correct graph will have the region below the curve y = 2^x shaded, indicating all points (x, y) where y is less than 2^x.
Related Videos
Related Practice
Textbook Question
525
views