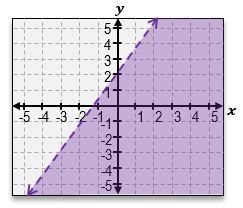
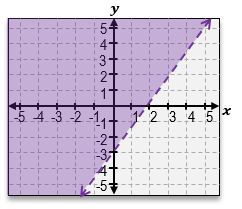
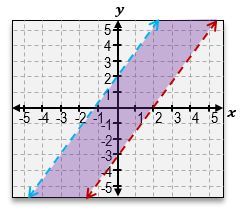
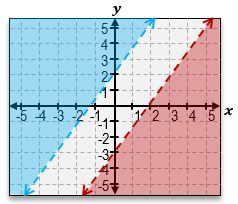
Graph the system of inequalities and indicate the region (if any) of solutions satisfying all equations.




$3x-2y>6$
$3x-2y$ < $-4$

• A.
• B.
• C.
• D.

Answer: (D)

Verified step by step guidance

1. Start by rewriting each inequality in slope-intercept form (y = mx + b). For the first inequality, 3x - 2y > 6, solve for y to get y < (3/2)x - 3.
2. For the second inequality, 3x - 2y < -4, solve for y to get y > (3/2)x + 2.
3. Graph the line y = (3/2)x - 3. Since the inequality is 'less than', use a dashed line and shade below the line.
4. Graph the line y = (3/2)x + 2. Since the inequality is 'greater than', use a dashed line and shade above the line.
5. The solution to the system of inequalities is the region where the shaded areas overlap. In this case, it is the region between the two lines.