Graph the solution set of each system of inequalities or indicate that the system has no solution.
$\begin{cases}y > 2x - 3 \\y < -x + 6\end{cases}$

Verified step by step guidance

1. Identify the two inequalities in the system: \(y > 4x - 2\) and \(y < -3x + 9\).
2. Graph the boundary lines for each inequality: the line \(y = 4x - 2\) and the line \(y = -3x + 9\). Use a solid line if the inequality includes equality (≥ or ≤), but here use dashed lines because the inequalities are strict ( > and < ).
3. Determine the shading for each inequality: For \(y > 4x - 2\), shade the region above the line \(y = 4x - 2\). For \(y < -3x + 9\), shade the region below the line \(y = -3x + 9\).
4. Find the intersection of the two shaded regions. This overlapping area represents the solution set to the system of inequalities.
5. If the shaded regions do not overlap, then the system has no solution. Otherwise, the solution set is the region where both inequalities are true simultaneously.

Key Concepts

Graphing Linear Inequalities

Graphing linear inequalities involves plotting the boundary line given by the corresponding linear equation and then shading the region that satisfies the inequality. For strict inequalities (>, <), the boundary line is dashed to indicate points on the line are not included. The shaded area represents all solutions that make the inequality true.

System of Inequalities

A system of inequalities consists of two or more inequalities considered simultaneously. The solution set is the intersection of the individual solution regions, meaning only points that satisfy all inequalities are included. If no common region exists, the system has no solution.

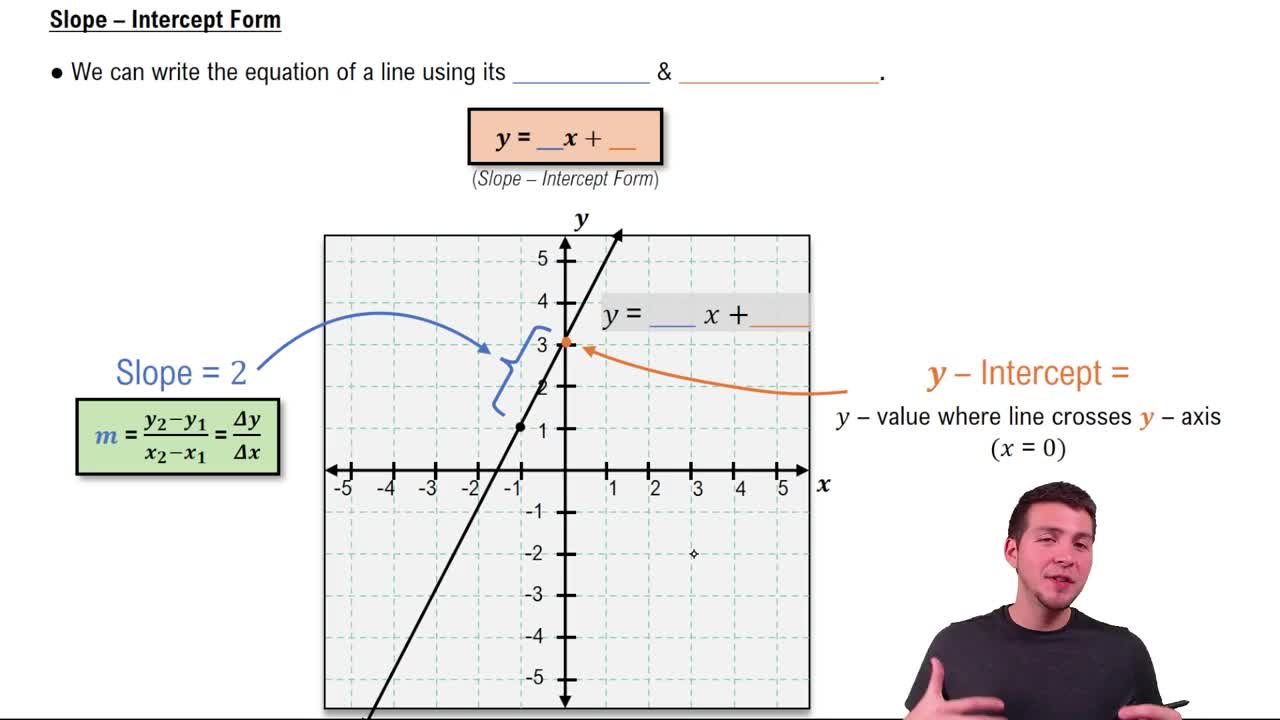
Slope-Intercept Form and Interpretation

The slope-intercept form y = mx + b expresses a line where m is the slope and b is the y-intercept. Understanding the slope helps determine the line's direction, while the intercept shows where it crosses the y-axis. This form is essential for quickly graphing the boundary lines of inequalities.