In trigonometry, the cosecant and secant functions are essential extensions of the sine and cosine functions, respectively. Understanding their graphs involves recognizing that cosecant is the reciprocal of sine, expressed mathematically as csc(x) = 1/sin(x), and secant is the reciprocal of cosine, given by sec(x) = 1/cos(x). This relationship is crucial for graphing these functions effectively.
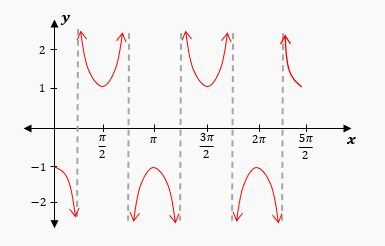
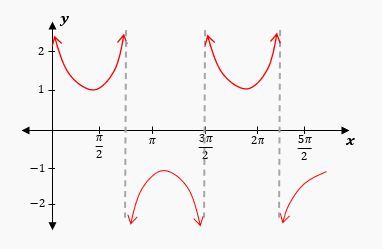
When graphing the cosecant function, it is important to note that it is undefined wherever the sine function equals zero, which occurs at integer multiples of π (i.e., 0, π, 2π, ...). At these points, vertical asymptotes are drawn, indicating that the cosecant function approaches infinity. For example, at x = 0, π, and 2π, the cosecant function is undefined. The behavior of the cosecant graph can be visualized as "smiley" and "frowny" faces, where the peaks correspond to the maximum values of the sine function and the valleys correspond to the minimum values.
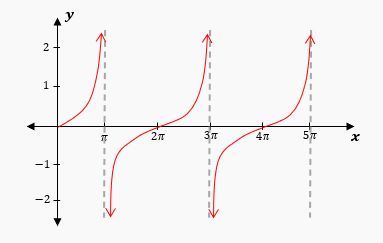
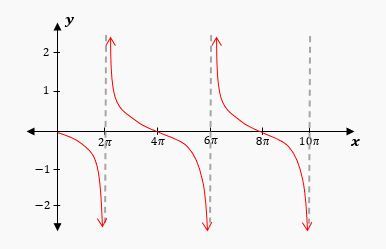
Similarly, the secant function is undefined wherever the cosine function equals zero, which occurs at odd multiples of π/2 (i.e., π/2, 3π/2, ...). As with cosecant, vertical asymptotes are placed at these points. The secant graph also exhibits a similar pattern of peaks and valleys, but the locations of the asymptotes differ from those of the cosecant function.
Both cosecant and secant functions can be transformed using the same rules applied to sine and cosine functions, such as stretching and shifting. For instance, to graph y = csc(2x), one would first graph y = sin(2x) to determine the key points and asymptotes. The period of the sine function is calculated using the formula Period = 2π/b, where b is the coefficient of x. In this case, with b = 2, the period becomes π.
After identifying the sine graph's peaks and zeros, the cosecant graph can be constructed by placing asymptotes at the zeros of the sine function and drawing the characteristic "smiley" and "frowny" shapes between these asymptotes. This method allows for a clear understanding of the behavior of both cosecant and secant functions, reinforcing their relationship with sine and cosine.