Determine the value of y = sin ⁡ ( − π 2 ) + 50 y=\sin\left(-\frac{\pi}{2}\right)+50 y = sin ( − 2 π ) + 50 without using a calculator or the unit circle.

y = 50 + 3 2 y=50+\frac{\sqrt3}{2} y = 50 + 2 3 <path d="M95,702 c-2.7,0,-7.17,-2.7,-13.5,-8c-5.8,-5.3,-9.5,-10,-9.5,-14 c0,-2,0.3,-3.3,1,-4c1.3,-2.7,23.83,-20.7,67.5,-54 c44.2,-33.3,65.8,-50.3,66.5,-51c1.3,-1.3,3,-2,5,-2c4.7,0,8.7,3.3,12,10 s173,378,173,378c0.7,0,35.3,-71,104,-213c68.7,-142,137.5,-285,206.5,-429 c69,-144,104.5,-217.7,106.5,-221 l0 -0 c5.3,-9.3,12,-14,20,-14 H400000v40H845.2724 s-225.272,467,-225.272,467s-235,486,-235,486c-2.7,4.7,-9,7,-19,7 c-6,0,-10,-1,-12,-3s-194,-422,-194,-422s-65,47,-65,47z M834 80h400000v40h-400000z">

The Period for the function y = cos ⁡ ( b x ) y=\cos\left(bx\right) y = cos ( b x ) is T = 20 π T=20\pi T = 20 π . Determine the correct value of b.

b = 1 10 b=\frac{1}{10} b = 10 1

b = 1 20 b=\frac{1}{20} b = 20 1

Describe the phase shift for the following function: y = cos ⁡ ( 5 x − π 2 ) y=\cos\left(5x-\frac{\pi}{2}\right) y = cos ( 5 x − 2 π )

π 10 \frac{\pi}{10} 10 π to the right

π 2 \frac{\pi}{2} 2 π to the right

π 2 \frac{\pi}{2} 2 π to the left

π 10 \frac{\pi}{10} 10 π to the left

Describe the phase shift for the following function: y = cos ⁡ ( 2 x + π 6 ) y=\cos\left(2x+\frac{\pi}{6}\right) y = cos ( 2 x + 6 π )

π 12 \frac{\pi}{12} 12 π to the left

π 6 \frac{\pi}{6} 6 π to the right

π 6 \frac{\pi}{6} 6 π to the left

π 12 \frac{\pi}{12} 12 π to the right

12. Trigonometric Functions

Graphs of Sine & Cosine

12. Trigonometric Functions

Graphs of Sine & Cosine: Videos & Practice Problems

Video Lessons Practice Worksheet

Topic summary

Understanding the sine and cosine functions involves recognizing their wave patterns, which can be transformed through vertical shifts, amplitude changes, reflections, and phase shifts. The amplitude indicates the height of the peaks, while the period defines the width of the wave, calculated as $P = \frac{2}{b}$ . A phase shift occurs when a constant is added or subtracted within the function, shifting the graph horizontally. Mastering these concepts is essential for graphing and analyzing trigonometric functions effectively.

concept

Graph of Sine and Cosine Function

Video duration:

Graph of Sine and Cosine Function Video Summary

Understanding the sine and cosine functions is essential for graphing these trigonometric functions on a standard x-y graph. The sine function corresponds to the y-coordinates on the unit circle, while the cosine function relates to the x-coordinates. As you traverse the unit circle, the values of sine and cosine repeat, leading to a wave-like pattern in their graphs.

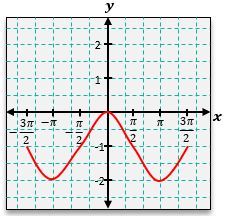
To graph the sine function, y = \sin(x), you can start by plotting key points based on the unit circle. For example, at x = 0, y = \sin(0) = 0; at x = \frac{\pi}{2}, y = \sin\left(\frac{\pi}{2}\right) = 1; at x = \pi, y = \sin(\pi) = 0; and at x = \frac{3\pi}{2}, y = \sin\left(\frac{3\pi}{2}\right) = -1. Continuing this process reveals that the sine graph oscillates between -1 and 1, creating a smooth wave pattern.

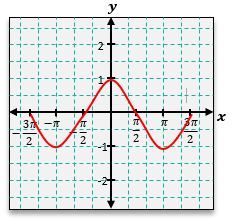
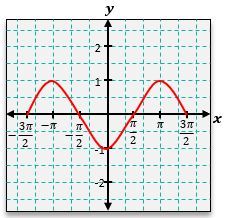
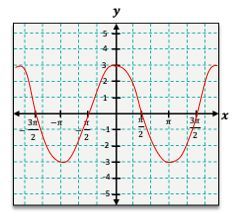
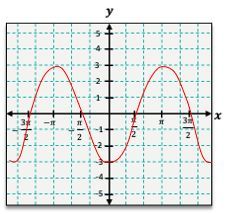
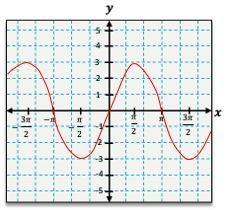
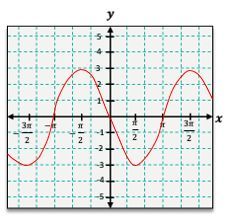
Similarly, the cosine function, y = \cos(x), can be graphed using its corresponding points. At x = 0, y = \cos(0) = 1; at x = \frac{\pi}{2}, y = \cos\left(\frac{\pi}{2}\right) = 0; at x = \pi, y = \cos(\pi) = -1; and at x = \frac{3\pi}{2}, y = \cos\left(\frac{3\pi}{2}\right) = 0. The cosine graph also exhibits a wave pattern, but it starts at a maximum value of 1, contrasting with the sine graph that begins at 0.

In wave terminology, the highest points of the graph are referred to as crests or peaks, while the lowest points are known as troughs or valleys. These peaks and valleys can vary in height depending on transformations applied to the sine and cosine functions.

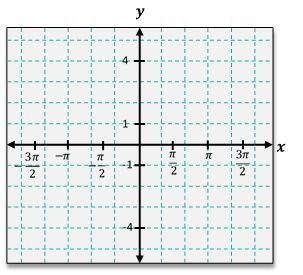
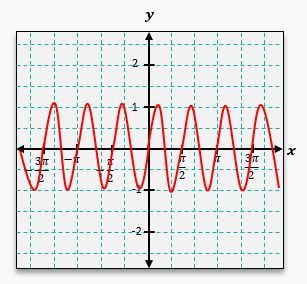
One common transformation is the vertical shift, which occurs when a constant k is added to the function. For instance, if you have y = \sin(x) + 1, the entire graph of y = \sin(x) shifts upward by 1 unit. This means that the original peaks and valleys will also adjust accordingly. The peak that was at 1 will now be at 2, and the valley that was at -1 will rise to 0.

To summarize, graphing sine and cosine functions involves understanding their periodic nature and how to plot key points derived from the unit circle. Additionally, recognizing how transformations like vertical shifts affect the graphs is crucial for accurately representing these functions. Mastering these concepts will enhance your ability to analyze and interpret trigonometric graphs effectively.

Problem

Sketch the function $y=\cos\left(x\right)-1$ on the graph below.

A cosine graph

Problem

Determine the value of $y=\sin\left(-\frac{\pi}{2}\right)+50$ without using a calculator or the unit circle.

$y=50$

$y=51$

$y=49$

$y=50+\frac{\sqrt3}{2}$

example

Graph of Sine and Cosine Function Example 1

Video duration:

Graph of Sine and Cosine Function Example 1 Video Summary

To graph the function $ y = \sin(x) + 3 $, it is beneficial to start with the basic sine function, $ y = \sin(x) $. The sine function is characterized by its wave-like pattern, beginning at the origin (0,0), reaching a peak at $ \frac{\pi}{2} $ (1), crossing the x-axis at $ \pi $ (0), reaching a valley at $ \frac{3\pi}{2} $ (-1), and continuing this oscillation indefinitely in both directions.

The sine wave oscillates between a maximum value of 1 and a minimum value of -1. When graphing $ y = \sin(x) + 3 $, the addition of 3 results in a vertical shift of the entire sine wave upwards by 3 units. This means that every point on the original sine graph will be moved up by 3 units.

For example, the starting point of the sine function at (0,0) will now be at (0,3). The peak that was originally at ( $ \frac{\pi}{2}, 1 $ ) will shift to ( $ \frac{\pi}{2}, 4 $ ), and the x-intercept at ( $ \pi, 0 $ ) will move to ( $ \pi, 3 $ ). Similarly, the valley at ( $ \frac{3\pi}{2}, -1 $ ) will now be at ( $ \frac{3\pi}{2}, 2 $ ).

Continuing this pattern, the graph will maintain its wave-like behavior, but all points will be elevated by 3 units. Thus, the new coordinates for key points will be as follows:

Starting point: (0, 3)
Peak: ( $ \frac{\pi}{2}, 4 $ )
X-intercept: ( $ \pi, 3 $ )
Valley: ( $ \frac{3\pi}{2}, 2 $ )

As you continue to graph this function, you will see the wave pattern extending infinitely in both directions, maintaining the same frequency and amplitude, but shifted vertically. This results in a complete graph of $ y = \sin(x) + 3 $ that reflects the original sine wave, simply elevated by 3 units across the entire x-axis.

concept

Amplitude and Reflection of Sine and Cosine

Video duration:

Amplitude and Reflection of Sine and Cosine Video Summary

In exploring the transformations of sine and cosine functions, we focus on two key concepts: amplitude and reflection. The amplitude of a function is defined as the distance from the midline of the graph to its peaks or valleys. For sine and cosine functions, which are periodic and oscillate, the amplitude can be determined by identifying this distance. For instance, if the amplitude is 1, the peaks will reach 1 unit above the midline and -1 unit below it.

When the amplitude is altered by a coefficient, such as multiplying the sine function by 2, the graph undergoes a vertical stretch. This means that the peaks and valleys of the graph will be twice as high and twice as low, respectively. For example, the function y = 2 \sin(x) will have an amplitude of 2, resulting in a graph that is taller than the standard sine wave.

Conversely, if the amplitude is negative, such as in the function y = -\sin(x), the graph is reflected over the x-axis. This reflection means that all positive values of the sine function become negative, effectively flipping the graph upside down. The transformation can be visualized by plotting points and connecting them smoothly, revealing the new orientation of the wave.

To illustrate both amplitude change and reflection, consider the function y = -\frac{3}{2} \cos(x). Here, the amplitude is 1.5, and the negative sign indicates a reflection over the x-axis. The cosine function typically starts at its maximum value, but due to the negative coefficient, it will start at a minimum value instead. As the graph progresses, it will reach a peak at x = \pi and return to a minimum at x = 2\pi, creating a wave that oscillates between -1.5 and 0.

Understanding these transformations allows for a deeper comprehension of how sine and cosine functions behave under various modifications, reinforcing the connection to algebraic transformations previously learned.

Problem

Determine the value of $y=-2\cdot\sin\left(-\frac{3\pi}{2}\right)+10$ without using a calculator or the unit circle.

$y=8$

$y=10$

$y=-2$

$y=12$

Problem

Graph the function $y=-3\cdot\cos\left(x\right)$ .

Graphing coordinate

Graph of y = -3 cos(x) showing the cosine function with amplitude -3.

Graphing coordinate

example

Amplitude and Reflection of Sine and Cosine Example 2

Video duration:

Amplitude and Reflection of Sine and Cosine Example 2 Video Summary

To graph the function $ y = 2 \sin(x) - 1 $, it's effective to first understand the basic sine function and then apply transformations. The sine function, $ y = \sin(x) $, oscillates between -1 and 1, with a period of $ 2\pi $. When we multiply the sine function by 2, as in $ y = 2 \sin(x) $, we alter the amplitude, causing the peaks to reach 2 and the valleys to drop to -2. This means the graph will oscillate between -2 and 2.

Starting from the centerline at $ y = 0 $, the peaks occur at $ \frac{\pi}{2} $ (where $ y = 2 $), and the valleys occur at $ \frac{3\pi}{2} $ (where $ y = -2 $). The graph continues this wave pattern indefinitely in both directions, reaching a valley at $ -\frac{\pi}{2} $ and a peak at $ -\frac{3\pi}{2} $.

Next, we incorporate the vertical shift introduced by the $-1$ in the function $ y = 2 \sin(x) - 1 $. This shift moves the entire graph down by one unit. Consequently, the new centerline is at $ y = -1 $. The peaks, originally at $ y = 2 $, are now at $ y = 1 $, and the valleys, originally at $ y = -2 $, are now at $ y = -3 $.

To visualize this, we start at the new centerline of $ y = -1 $. The peak at $ \frac{\pi}{2} $ is now at $ y = 1 $, and the graph crosses the centerline back down to $ y = -1 $ at $ x = \pi $. The valley at $ \frac{3\pi}{2} $ is now at $ y = -3 $. Extending this to the left, the valley at $ -\frac{\pi}{2} $ is at $ y = -3 $, the centerline is crossed at $ -\pi $ (where $ y = -1 $), and the peak at $ -\frac{3\pi}{2} $ is at $ y = 1 $.

In summary, the graph of $ y = 2 \sin(x) - 1 $ oscillates between $ y = 1 $ and $ y = -3 $, with a centerline at $ y = -1 $, maintaining the sine wave's periodic nature while reflecting the transformations applied. This understanding of amplitude changes and vertical shifts is crucial for accurately graphing trigonometric functions.

concept

Period of Sine and Cosine Functions

Video duration:

Period of Sine and Cosine Functions Video Summary

Understanding the sine and cosine functions is essential in trigonometry, particularly when analyzing their graphs. Two key characteristics of these functions are amplitude and period. While amplitude indicates the height of the graph, the period describes the width of the graph, specifically the distance along the x-axis required to complete one full cycle of the wave.

The standard sine function, y = sin(x), has a period of 2\pi. This means that it takes 2\pi units along the x-axis to return to the starting point of the wave. To visualize this, one can observe the graph rising to a peak, descending back to zero, dropping to a trough, and returning to zero again, completing a full cycle.

When the function is modified, such as in y = sin(2x), the period changes. In this case, the graph completes its cycle in \pi units instead of 2\pi. The factor that modifies the period is represented by b, which is the coefficient in front of x within the sine or cosine function. The relationship between the period and b is given by the formula:

Period = \frac{2\pi}{b}

For the function y = sin(x), since b = 1, the period is:

Period = \frac{2\pi}{1} = 2\pi

For y = sin(2x), where b = 2, the period is:

Period = \frac{2\pi}{2} = \pi

When b is greater than 1, the graph horizontally shrinks, resulting in a shorter period. Conversely, if b is between 0 and 1, the graph stretches horizontally, leading to a longer period.

To further illustrate this concept, consider two examples. For the function y = sin(\frac{1}{2}x), the value of b is \frac{1}{2}. Applying the period formula:

Period = \frac{2\pi}{\frac{1}{2}} = 2\pi \times 2 = 4\pi

For the function y = cos(4\pi x), the value of b is 4\pi. Thus, the period is calculated as:

Period = \frac{2\pi}{4\pi} = \frac{1}{2}

These calculations demonstrate how to determine the period of sine and cosine functions without graphing, reinforcing the understanding of how the coefficient in front of x affects the graph's width. Mastery of these concepts is crucial for solving problems related to periodic functions in trigonometry.

Problem

Given below is the graph of the function $y=\sin\left(bx\right)$ . Determine the correct value for b.

$b=\pi$

$b=2$

$b=\frac12$

$b=4$

Problem

The Period for the function $y=\cos\left(bx\right)$ is $T=20\pi$ . Determine the correct value of b.

$b=\frac{1}{10}$

$b=10$

$b=20$

$b=\frac{1}{20}$

concept

Phase Shifts

Video duration:

Phase Shifts Video Summary

Understanding the transformations of sine and cosine functions is essential in trigonometry, particularly when it comes to phase shifts. A phase shift refers to a horizontal shift of the graph, which can occur to the left or right, similar to how a vertical shift moves the graph up or down.

To illustrate a phase shift, consider the cosine function, y = \cos(x). When a number is added or subtracted inside the cosine function, such as in y = \cos(x - \frac{\pi}{2}), it results in a shift of the graph. For example, evaluating points for this function shows that the graph starts at zero instead of one, indicating a rightward shift of \frac{\pi}{2} units. This transformation can be visualized by plotting key points and connecting them smoothly, revealing that the entire wave has been shifted horizontally.

In general, if the function is in the form y = \cos(bx - h), the phase shift can be determined by the value of h. If h is positive, the graph shifts to the right by \frac{h}{b} units. Conversely, if the function is in the form y = \cos(bx + h), the graph shifts to the left by \frac{h}{b} units. For instance, in the function y = \cos(x - \frac{\pi}{2}), the phase shift is \frac{\pi}{2} to the right, as h = \frac{\pi}{2} and b = 1.

Another important aspect is the period of the function, which is determined by the coefficient b. The period of a sine or cosine function is given by the formula P = \frac{2\pi}{b}. For example, in the function y = \sin(2x), the period is \frac{2\pi}{2} = \pi, indicating that the graph completes one full cycle over the interval from 0 to \pi.

When analyzing a function like y = \sin(2x + \pi), the phase shift can be calculated as follows: since it is in the form y = \sin(bx + h), where h = \pi and b = 2, the graph shifts left by \frac{\pi}{2} units. This means that the starting point of the sine wave will be adjusted accordingly, affecting the overall shape and position of the graph.

In summary, phase shifts are a crucial concept in understanding the behavior of sine and cosine functions. By recognizing how the addition or subtraction of values within the function affects the graph's position, students can better visualize and analyze trigonometric functions.

13

Problem

Describe the phase shift for the following function:
 $y=\cos\left(5x-\frac{\pi}{2}\right)$

A

$\frac{\pi}{2}$ to the right

B

$\frac{\pi}{2}$ to the left

C

$\frac{\pi}{10}$ to the right

D

$\frac{\pi}{10}$ to the left

14

Problem

Describe the phase shift for the following function:
 $y=\cos\left(2x+\frac{\pi}{6}\right)$

A

$\frac{\pi}{6}$ to the right

B

$\frac{\pi}{6}$ to the left

C

$\frac{\pi}{12}$ to the right

D

$\frac{\pi}{12}$ to the left

15

example

`Phase Shifts Example 3`

Video duration: 
3m

Play a video:

`Phase Shifts Example 3 Video Summary`

To graph the function \( y = 3 \sin(x + \pi) \), we start by identifying the general form of the sine function, which is expressed as \( y = a \sin(bx - h) + k \). In this case, we can see that the amplitude \( a \) is 3, indicating that the graph will oscillate between 3 and -3 on the y-axis. The absence of a vertical shift means \( k = 0 \).
Next, we analyze the term \( x + \pi \). To fit this into the general form, we rewrite it as \( x - (-\pi) \). This reveals that \( h = -\pi \). The phase shift can be calculated using the formula \( \frac{h}{b} \). Here, \( b = 1 \) (since there is no coefficient in front of \( x \)), leading to a phase shift of \( \frac{-\pi}{1} = -\pi \). This indicates a shift of \( \pi \) units to the left.
Now, we can graph the basic sine function \( y = 3 \sin(x) \). The standard sine graph starts at the origin, reaches a peak of 3 at \( \frac{\pi}{2} \), crosses the x-axis at \( \pi \), and reaches a valley of -3 at \( \frac{3\pi}{2} \). This pattern continues indefinitely in both directions.
Incorporating the phase shift, we adjust the graph to the left by \( \pi \) units. The new key points will be as follows: the peak at \( -\frac{\pi}{2} \) (where \( y = 3 \)), crossing through \( -\pi \) (where \( y = 0 \)), and reaching a valley at \( -\frac{3\pi}{2} \) (where \( y = -3 \)). Continuing this pattern, we find that the graph will also peak at \( \frac{\pi}{2} \) and cross through \( \pi \) as it moves to the right.
In summary, the graph of \( y = 3 \sin(x + \pi) \) oscillates between 3 and -3, with a phase shift of \( \pi \) units to the left, resulting in a modified sine wave that starts at the center and follows the established sine wave pattern.

`Do you want more practice?`

We have more practice problems on Graphs of Sine & Cosine

`Here’s what students ask on this topic:`

What is the difference between the graphs of sine and cosine functions?

The sine and cosine functions both produce wave-like graphs, but they differ in their starting points. The sine graph, y = sin(x), begins at the origin (0, 0), while the cosine graph, y = cos(x), starts at its maximum value (0, 1). Both graphs have the same amplitude (height of the wave) and period (length of one complete cycle), typically 2π for their standard forms. The sine graph is symmetric about the origin, making it an odd function, while the cosine graph is symmetric about the y-axis, making it an even function. These differences arise because sine corresponds to the y-coordinate and cosine to the x-coordinate on the unit circle. Despite these distinctions, their wave patterns are identical, just horizontally shifted by π/2 radians.

How do you calculate the period of a sine or cosine function?

The period of a sine or cosine function determines the length of one complete wave cycle along the x-axis. It is calculated using the formula:
 $P = \frac{2}{b}$ 
Here, b is the coefficient of x inside the sine or cosine function. For example, in y = sin(2x), b = 2. Substituting into the formula, the period is:
 $P = \frac{2}{2} = π$ 
This means the wave completes one cycle in π units. If b is less than 1, the graph stretches horizontally, increasing the period. If b is greater than 1, the graph compresses, decreasing the period.

What is the amplitude of a sine or cosine function, and how is it determined?

The amplitude of a sine or cosine function represents the height of the wave from its midline to its peak or trough. It is determined by the absolute value of the coefficient in front of the sine or cosine function. For example, in y = 3sin(x), the amplitude is |3| = 3. Similarly, in y = -2cos(x), the amplitude is |−2| = 2. The amplitude affects the vertical stretch or compression of the graph but does not change the period or phase shift. A larger amplitude results in taller waves, while a smaller amplitude produces shorter waves. If the coefficient is negative, the graph is reflected over the x-axis, but the amplitude remains positive.

What is a phase shift in the graphs of sine and cosine functions?

A phase shift is a horizontal shift of the sine or cosine graph along the x-axis. It occurs when a constant is added or subtracted inside the function's argument. For example, in y = sin(x − π/2), the graph shifts to the right by π/2 units. The general form for phase shift is determined by the equation:
 $Phase Shift = \frac{h}{b}$ 
Here, h is the constant added or subtracted, and b is the coefficient of x. If h is positive, the graph shifts to the left; if h is negative, it shifts to the right. For example, in y = cos(2x + π), the phase shift is:
 $- \frac{π}{2}$ 
This means the graph shifts left by π/2 units.

How do vertical shifts affect the graphs of sine and cosine functions?

Vertical shifts move the sine or cosine graph up or down along the y-axis. This occurs when a constant k is added or subtracted to the function. For example, in y = sin(x) + 2, the entire graph shifts up by 2 units. Similarly, in y = cos(x) − 3, the graph shifts down by 3 units. The midline of the graph, which is usually y = 0, becomes y = k. Vertical shifts do not affect the amplitude, period, or phase shift of the graph; they only change the vertical position. To graph a vertically shifted function, plot the standard sine or cosine graph first, then move all points up or down by the value of k.

What happens to the sine or cosine graph when the amplitude is negative?

When the amplitude of a sine or cosine function is negative, the graph is reflected over the x-axis. For example, in y = −sin(x), the wave pattern of the sine graph flips upside down. Peaks become troughs, and troughs become peaks. However, the amplitude, which is the absolute value of the coefficient, remains positive. For instance, in y = −3cos(x), the amplitude is |−3| = 3, but the graph is inverted. This reflection does not affect the period, phase shift, or vertical shift of the graph; it only changes the orientation of the wave.

`Your Business Calculus tutors`


Callie
Math Instructor


Nick
Math Instructor

Graphs of Sine & Cosine: Videos & Practice Problems

Graph of Sine and Cosine Function

Graph of Sine and Cosine Function Video Summary

Sketch the function y=cos(x)−1y=\cos\left(x\right)-1y=cos(x)−1 on the graph below.

Determine the value of y=sin(−π2)+50y=\sin\left(-\frac{\pi}{2}\right)+50y=sin(−2π)+50 without using a calculator or the unit circle.

Graph of Sine and Cosine Function Example 1

Graph of Sine and Cosine Function Example 1 Video Summary

Amplitude and Reflection of Sine and Cosine

Amplitude and Reflection of Sine and Cosine Video Summary

Determine the value of y=−2⋅sin(−3π2)+10y=-2\cdot\sin\left(-\frac{3\pi}{2}\right)+10y=−2⋅sin(−23π)+10 without using a calculator or the unit circle.

Graph the function y=−3⋅cos(x)y=-3\cdot\cos\left(x\right)y=−3⋅cos(x).

Amplitude and Reflection of Sine and Cosine Example 2

Amplitude and Reflection of Sine and Cosine Example 2 Video Summary

Period of Sine and Cosine Functions

Period of Sine and Cosine Functions Video Summary

Given below is the graph of the function y=sin(bx)y=\sin\left(bx\right)y=sin(bx). Determine the correct value for b.

The Period for the function y=cos(bx)y=\cos\left(bx\right)y=cos(bx) is T=20πT=20\piT=20π. Determine the correct value of b.

Phase Shifts

Phase Shifts Video Summary

Describe the phase shift for the following function:y=cos(5x−π2)y=\cos\left(5x-\frac{\pi}{2}\right)y=cos(5x−2π)

Describe the phase shift for the following function:y=cos(2x+π6)y=\cos\left(2x+\frac{\pi}{6}\right)y=cos(2x+6π)

Phase Shifts Example 3

Phase Shifts Example 3 Video Summary

Do you want more practice?

Here’s what students ask on this topic:

What is the difference between the graphs of sine and cosine functions?

How do you calculate the period of a sine or cosine function?

What is the amplitude of a sine or cosine function, and how is it determined?

What is a phase shift in the graphs of sine and cosine functions?

How do vertical shifts affect the graphs of sine and cosine functions?

What happens to the sine or cosine graph when the amplitude is negative?

Your Business Calculus tutors

Sketch the function $y=\cos\left(x\right)-1$ on the graph below.

Determine the value of $y=\sin\left(-\frac{\pi}{2}\right)+50$ without using a calculator or the unit circle.

Determine the value of $y=-2\cdot\sin\left(-\frac{3\pi}{2}\right)+10$ without using a calculator or the unit circle.

Graph the function $y=-3\cdot\cos\left(x\right)$ .

Given below is the graph of the function $y=\sin\left(bx\right)$ . Determine the correct value for b.

The Period for the function $y=\cos\left(bx\right)$ is $T=20\pi$ . Determine the correct value of b.

Describe the phase shift for the following function:
$y=\cos\left(5x-\frac{\pi}{2}\right)$

Describe the phase shift for the following function:
$y=\cos\left(2x+\frac{\pi}{6}\right)$

`Phase Shifts Example 3`

`Phase Shifts Example 3 Video Summary`

`Do you want more practice?`

`Here’s what students ask on this topic:`

`Your Business Calculus tutors`