Trigonometric Functions on the Unit Circle: Videos & Practice Problems

The unit circle is essential for understanding trigonometric functions, where angles correspond to specific x and y coordinates. The sine and cosine of an angle are represented by the y and x values, respectively, while tangent is the ratio of sine to cosine. For angles outside the first quadrant, reference angles simplify calculations. Reciprocal functions like cosecant, secant, and cotangent are derived from sine, cosine, and tangent. Key equations include the unit circle equation $x^2+y^2=1$.

Introduction to the Unit Circle

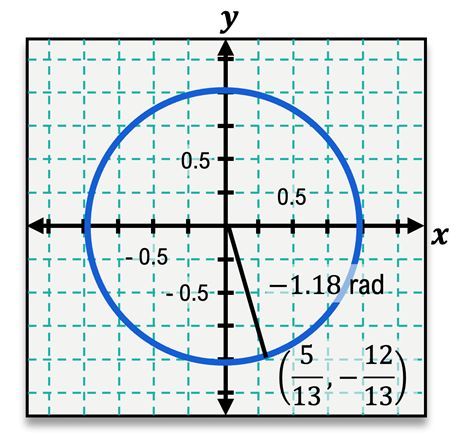
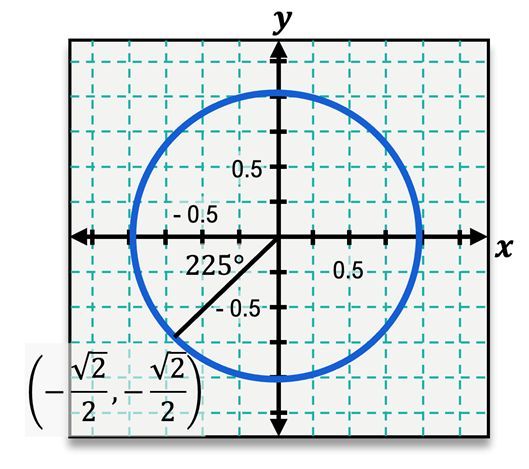
The unit circle is a fundamental concept in trigonometry, defined as a circle with a radius of one centered at the origin (0, 0) of a coordinate plane. It serves as a crucial tool for solving various trigonometric problems. The angles around the unit circle are measured in both degrees and radians, with a full rotation of 360 degrees corresponding to \(2\pi\) radians. The key angle measures include:

• 0 degrees (0 radians) at the point (1, 0)
• 90 degrees (\(\frac{\pi}{2}\) radians) at the point (0, 1)
• 180 degrees (\(\pi\) radians) at the point (-1, 0)
• 270 degrees (\(\frac{3\pi}{2}\) radians) at the point (0, -1)
• 360 degrees (\(2\pi\) radians) at the point (1, 0)

Each angle on the unit circle corresponds to specific coordinates (x, y) that can be derived from the circle's equation, which is given by:

\(x^2 + y^2 = 1\)

This equation indicates that any point (x, y) on the unit circle satisfies this relationship. To determine if a point lies on the unit circle, one can substitute the coordinates into the equation. For example, to check if the point (1, 1) is on the unit circle:

Substituting gives:

\(1^2 + 1^2 = 1 + 1 = 2\) (not equal to 1, so it is not on the unit circle).

In contrast, for the point \(\left(\frac{1}{2}, \frac{\sqrt{3}}{2}\right)\):

Substituting gives:

\(\left(\frac{1}{2}\right)^2 + \left(\frac{\sqrt{3}}{2}\right)^2 = \frac{1}{4} + \frac{3}{4} = 1\) (equal to 1, so it is on the unit circle).

Additionally, every point on the unit circle corresponds to a specific angle. For instance, the point \(\left(\frac{1}{2}, \frac{\sqrt{3}}{2}\right)\) corresponds to an angle of 60 degrees (or \(\frac{\pi}{3}\) radians). Understanding the unit circle and its properties is essential for mastering trigonometric functions and their applications.

Identify the quadrant that the given angle is located in.
$\frac{7\pi}{4}$ radians

• A. Quadrant I
• B. Quadrant II
• C. Quadrant III
• D. Quadrant IV

Answer: (D)

Identify the quadrant that the given angle is located in.
$\frac{\pi}{7}$ radians

• A. Quadrant I
• B. Quadrant II
• C. Quadrant III
• D. Quadrant IV

Answer: (A)

Identify the quadrant that the given angle is located in.
$\frac{2\pi}{3}$ radians

• A. Quadrant I
• B. Quadrant II
• C. Quadrant III
• D. Quadrant IV

Answer: (B)

Identify the quadrant that the given angle is located in.
$\frac{6\pi}{5}$ radians

• A. Quadrant I
• B. Quadrant II
• C. Quadrant III
• D. Quadrant IV

Answer: (C)

Test whether the point is on the unit circle by plugging it into the equation, $x^2+y^2=1$.
$\left(\frac{-\sqrt2}{2},\frac{-\sqrt2}{2}\right)$

• A. On Unit Circle
• B. NOT on Unit Circle
• C. More information is required

Answer: (A)

Sine, Cosine, & Tangent on the Unit Circle

The unit circle is a fundamental concept in trigonometry, where each angle corresponds to a specific point defined by coordinates (x, y). For example, an angle of 0 degrees corresponds to the point (1, 0). The relationship between angles and these coordinates is established through trigonometric functions: sine, cosine, and tangent. These functions can be understood in the context of right triangles formed by the radius of the unit circle, which is always 1.

For any angle θ, the sine function is defined as the y-coordinate (height) of the corresponding point on the unit circle, while the cosine function is defined as the x-coordinate (base). This can be remembered by the alphabetical order of the functions: cosine (c) comes before sine (s), indicating that cosine corresponds to the x-value and sine to the y-value. For instance, for an angle of 53 degrees, if the coordinates are (3/5, 4/5), then:

$$\sin(53^\circ) = \frac{4}{5}$$

$$\cos(53^\circ) = \frac{3}{5}$$

To find the tangent of an angle, you can use the relationship:

$$\tan(θ) = \frac{\sin(θ)}{\cos(θ)} = \frac{y}{x}$$

For example, at 0 degrees, the sine is 0 and the cosine is 1, leading to:

$$\tan(0^\circ) = \frac{0}{1} = 0$$

At 90 degrees, the sine is 1 and the cosine is 0, resulting in an undefined tangent since division by zero is not possible. Similarly, at 180 degrees, the sine is 0 and the cosine is -1, giving:

$$\tan(180^\circ) = \frac{0}{-1} = 0$$

At 270 degrees, the sine is -1 and the cosine is 0, which again results in an undefined tangent.

Moving to angles in different quadrants, such as 217 degrees, the coordinates might be (-4/5, -3/5). Here, the sine and cosine values are negative, reflecting their positions in the third quadrant:

$$\sin(217^\circ) = -\frac{3}{5}$$

$$\cos(217^\circ) = -\frac{4}{5}$$

$$\tan(217^\circ) = \frac{-\frac{3}{5}}{-\frac{4}{5}} = \frac{3}{4}$$

For angles like 60 degrees in the first quadrant, the coordinates are (1/2, √3/2), leading to:

$$\sin(60^\circ) = \frac{\sqrt{3}}{2}$$

$$\cos(60^\circ) = \frac{1}{2}$$

$$\tan(60^\circ) = \frac{\frac{\sqrt{3}}{2}}{\frac{1}{2}} = \sqrt{3}$$

Understanding these relationships allows for easier calculations of trigonometric values using the unit circle, reinforcing the connection between angles and their corresponding coordinates.

Find the sine, cosine, and tangent of each angle using the unit circle.
$\theta=-1.18$ rad, $\left(\frac{5}{13},-\frac{12}{13}\right)$

• A. $\sin\theta=-\frac{12}{13},\cos\theta=\frac{5}{13},\tan\theta=\frac{12}{5}$
• B. $\sin\theta=-\frac{12}{13},\cos\theta=\frac{5}{13},\tan\theta=-\frac{12}{5}$
• C. $\sin\theta=\frac{12}{13},\cos\theta=\frac{5}{13},\tan\theta=\frac{5}{12}$
• D. $\sin\theta=\frac{5}{13},\cos\theta=\frac{-12}{13},\tan\theta=\frac{5}{12}$

Answer: (B)

Find the sine, cosine, and tangent of each angle using the unit circle.
$\theta=225\degree,\left(-\frac{\sqrt2}{2},-\frac{\sqrt2}{2}\right)$

• A. $\sin\theta=-\frac{\sqrt2}{2},\cos\theta=-\frac{\sqrt2}{2},\tan\theta=2$
• B. $\sin\theta=\frac{\sqrt2}{2},\cos\theta=-\frac{\sqrt2}{2},\tan\theta=-1$
• C. $\sin\theta=-\frac{\sqrt2}{2},\cos\theta=-\frac{\sqrt2}{2},\tan\theta=1$
• D. $\sin\theta=\frac{\sqrt2}{2},\cos\theta=\frac{\sqrt2}{2},\tan\theta=\frac{\sqrt2}{1}$

Answer: (C)

Sine, Cosine, & Tangent of 30°, 45°, & 60°

Trigonometric functions establish a relationship between angles and their corresponding points on the unit circle, where the x and y coordinates represent the cosine and sine values of those angles, respectively. To effectively find the sine or cosine of common angles—specifically 30°, 45°, and 60°—it is essential to memorize their values, as they may not always be provided.

One effective method for memorization is known as the "one two three rule." This approach begins with the understanding that all sine and cosine values for these angles can be expressed as a fraction involving the square root of a number over two. The process starts at the angle of 60° and involves counting clockwise for x values (cosine) and counterclockwise for y values (sine). For instance, the cosine of 60° is derived from the x-coordinate, which is 1/2, while the sine of 30° corresponds to the y-coordinate, also 1/2. The tangent of an angle can be calculated by dividing the sine by the cosine. For 30°, this results in a tangent value of \( \frac{1}{\sqrt{3}} \), which can be rationalized to \( \frac{\sqrt{3}}{3} \).

Another practical method for memorizing these values is the "left hand rule." In this technique, your left hand represents the first quadrant of the unit circle, with your pinky at 0° and your thumb at 90°. The three fingers between them represent the angles 30°, 45°, and 60°. To find the sine and cosine values, you fold down the finger corresponding to the angle in question. For example, when determining the values for 30°, you would fold down the 30° finger and count the fingers above (3) for cosine, yielding \( \frac{\sqrt{3}}{2} \), and the fingers below (1) for sine, resulting in \( \frac{1}{2} \). The tangent can again be found by dividing sine by cosine or by counting fingers, leading to the same result of \( \frac{1}{\sqrt{3}} \) or \( \frac{\sqrt{3}}{3} \).

These memorization techniques provide a solid foundation for solving trigonometric problems involving these common angles, enhancing both understanding and application of trigonometric functions in various mathematical contexts.

Sine, Cosine, & Tangent of 30°, 45°, & 60° Example 1

Understanding the unit circle is essential for mastering trigonometry, particularly when it comes to angles and their corresponding sine, cosine, and tangent values. The unit circle is a circle with a radius of one, centered at the origin of a coordinate system, and it provides a visual representation of these trigonometric functions.

To begin filling in the first quadrant of the unit circle, start with the key points on the x and y axes. At 0 degrees (or 0 radians), the coordinates are (1, 0), and at 90 degrees (or π/2 radians), the coordinates are (0, 1). Next, identify the degree measures of 30 degrees, 45 degrees, and 60 degrees, which are crucial for determining their radian equivalents. The conversions are as follows:

• 30 degrees = π/6 radians
• 45 degrees = π/4 radians
• 60 degrees = π/3 radians

These conversions can be reasoned out based on their positions relative to 90 degrees. For example, 45 degrees is halfway between 0 and 90 degrees, leading to π/4, while 30 degrees is one-third of 90 degrees, resulting in π/6. Similarly, 60 degrees, being double 30 degrees, corresponds to π/3.

Next, we calculate the sine and cosine values for these angles. The sine and cosine values can be derived from the coordinates of the points on the unit circle:

• For 30 degrees: sin(30°) = 1/2, cos(30°) = √3/2
• For 45 degrees: sin(45°) = √2/2, cos(45°) = √2/2
• For 60 degrees: sin(60°) = √3/2, cos(60°) = 1/2

To find the tangent values, use the relationship that tangent is the ratio of sine to cosine (or y/x). Thus:

• tan(30°) = (1/2) / (√3/2) = 1/√3, which rationalizes to √3/3
• tan(45°) = (√2/2) / (√2/2) = 1
• tan(60°) = (√3/2) / (1/2) = √3
• tan(0°) = 0/1 = 0
• tan(90°) = 1/0 = undefined

In summary, the first quadrant of the unit circle is filled with the following key values:

• 0°: (1, 0), tan(0°) = 0
• 30°: (√3/2, 1/2), tan(30°) = √3/3
• 45°: (√2/2, √2/2), tan(45°) = 1
• 60°: (1/2, √3/2), tan(60°) = √3
• 90°: (0, 1), tan(90°) = undefined

Repetition and practice are key to mastering the unit circle, so revisiting these concepts frequently will help solidify your understanding. If you have any questions, don't hesitate to seek clarification.

Reference Angles on the Unit Circle

Understanding trigonometric values in all four quadrants of the unit circle is essential for mastering trigonometry. While we are familiar with the trig values for common angles in the first quadrant, we can extend this knowledge to angles in the other quadrants using the concept of reference angles. A reference angle is the acute angle formed by the terminal side of a given angle and the x-axis, which allows us to relate angles in other quadrants back to those in the first quadrant.

To find a reference angle, we measure the angle to the nearest x-axis. For example, for an angle of 150 degrees, the nearest x-axis is at 180 degrees. The difference between these two angles is 30 degrees, making the reference angle for 150 degrees equal to 30 degrees. Similarly, for 135 degrees, the nearest x-axis is also 180 degrees, and the difference is 45 degrees, giving it a reference angle of 45 degrees. For 120 degrees, the nearest x-axis is again 180 degrees, and the difference is 60 degrees, resulting in a reference angle of 60 degrees.

In the third quadrant, for an angle of 210 degrees, the nearest x-axis is 180 degrees, and the difference is 30 degrees, so the reference angle is 30 degrees. For 225 degrees, which is directly in the center of the quadrant, the reference angle is 45 degrees. For 240 degrees, the nearest x-axis is 180 degrees, and the difference is 60 degrees, giving it a reference angle of 60 degrees. In the fourth quadrant, for 330 degrees, the nearest x-axis is 360 degrees, and the difference is 30 degrees, resulting in a reference angle of 30 degrees. For 315 degrees, the reference angle is also 45 degrees, and for 300 degrees, it is 60 degrees.

To help remember these reference angles, one can visualize them forming an "X" shape. All angles with a reference angle of 30 degrees create one "X," while those with a reference angle of 45 degrees form another "X," and angles with a reference angle of 60 degrees create a taller, thinner "X." Additionally, when considering radian measures, angles with a reference angle of 30 degrees correspond to a denominator of 6, those with 45 degrees have a denominator of 4, and those with 60 degrees have a denominator of 3.

By mastering the concept of reference angles, students can efficiently determine trigonometric values for angles in all quadrants, reinforcing their understanding of the unit circle and its applications in trigonometry.

Identify the reference angle of each given angle.
120°

• A. 30°
• B. 45°
• C. 60°

Answer: (C)

Identify the reference angle of each given angle.
$\frac{7\pi}{4}$ rad

• A. $\frac{\pi}{6}$
• B. $\frac{\pi}{4}$
• C. $\frac{\pi}{3}$

Answer: (B)

Identify the reference angle of each given angle.
210°

• A. 30°
• B. 45°
• C. 60°

Answer: (A)

Trig Values in Quadrants II, III, & IV

Understanding the trigonometric values of angles in different quadrants is essential for mastering trigonometry. The key takeaway is that the sine, cosine, and tangent values of angles in quadrants two, three, and four can be derived from the reference angles in quadrant one, with adjustments made for their signs based on the quadrant's characteristics.

In quadrant one, all trigonometric values are positive. As we move to quadrant two, for example, the angle of 150 degrees has a reference angle of 30 degrees. The cosine and sine values remain the same as those of the reference angle, but the cosine becomes negative because it corresponds to the x-coordinate, which is negative in this quadrant. Thus, the values for 150 degrees are:

Cosine: \( -\frac{\sqrt{3}}{2} \), Sine: \( \frac{1}{2} \), Tangent: \( -\frac{\sqrt{3}}{3} \).

In quadrant three, the angle of 225 degrees has a reference angle of 45 degrees. Here, both the sine and cosine values are negative, while the tangent, being the ratio of sine to cosine, is positive. Therefore, the values for 225 degrees are:

Cosine: \( -\frac{\sqrt{2}}{2} \), Sine: \( -\frac{\sqrt{2}}{2} \), Tangent: \( 1 \).

Moving to quadrant four, the angle of 300 degrees has a reference angle of 60 degrees. In this quadrant, the cosine is positive while the sine is negative, leading to the following values:

Cosine: \( \frac{1}{2} \), Sine: \( -\frac{\sqrt{3}}{2} \), Tangent: \( -\frac{\sqrt{3}}{3} \).

To remember which trigonometric functions are positive in each quadrant, a helpful mnemonic is "All Students Take Calculus" (ASTC). This indicates that:

• Quadrant I: All functions are positive.
• Quadrant II: Sine is positive.
• Quadrant III: Tangent is positive.
• Quadrant IV: Cosine is positive.

By understanding these relationships and the signs of the trigonometric functions in each quadrant, you can effectively navigate the unit circle and apply these concepts to various problems in trigonometry.

Trig Values in Quadrants II, III, & IV Example 2

Understanding reference angles is essential for determining the values of trigonometric functions in different quadrants of the unit circle. Each quadrant has specific signs for sine, cosine, and tangent based on the mnemonic "All Students Take Calculus," which indicates which functions are positive in each quadrant.

In Quadrant II, we analyze angles such as 135 degrees and 120 degrees. The reference angles for these are 45 degrees and 60 degrees, respectively. The trigonometric values for 135 degrees are:

• Cosine: \(-\frac{\sqrt{2}}{2}\)
• Sine: \(\frac{\sqrt{2}}{2}\)
• Tangent: \(-1\)

For 120 degrees, the values are:

• Cosine: \(-\frac{1}{2}\)
• Sine: \(\frac{\sqrt{3}}{2}\)
• Tangent: \(-\frac{\sqrt{3}}{3}\)

In this quadrant, sine is positive while cosine and tangent are negative.

Moving to Quadrant III, we consider angles 210 degrees and 240 degrees, with reference angles of 30 degrees and 60 degrees. The trigonometric values for 210 degrees are:

• Cosine: \(-\frac{\sqrt{3}}{2}\)
• Sine: \(-\frac{1}{2}\)
• Tangent: \(\frac{\sqrt{3}}{3}\)

For 240 degrees, the values are:

• Cosine: \(-\frac{1}{2}\)
• Sine: \(-\frac{\sqrt{3}}{2}\)
• Tangent: \(\sqrt{3}\)

In this quadrant, only tangent is positive, while sine and cosine are negative.

Finally, in Quadrant IV, we examine angles 330 degrees and 315 degrees, which have reference angles of 30 degrees and 45 degrees. The trigonometric values for 330 degrees are:

• Cosine: \(\frac{\sqrt{3}}{2}\)
• Sine: \(-\frac{1}{2}\)
• Tangent: \(-\frac{\sqrt{3}}{3}\)

For 315 degrees, the values are:

• Cosine: \(\frac{\sqrt{2}}{2}\)
• Sine: \(-\frac{\sqrt{2}}{2}\)
• Tangent: -1

In this quadrant, cosine is positive while sine and tangent are negative.

By understanding the reference angles and the signs of the trigonometric functions in each quadrant, you can effectively determine the values needed for various angles on the unit circle. Practice these concepts to reinforce your understanding and application of trigonometric functions.

Identify what angle, $\theta$ , satisfies the following conditions.
$\sin\theta=\frac12$; $\tan\theta$ < $0$

• A. 30°
• B. 150°
• C. 60°
• D. 300°

Answer: (B)

Identify what angle, $\theta$ , satisfies the following conditions.
$\cos\theta=\frac{\sqrt3}{2}$; $\sin\theta$ < $0$

• A. 30°
• B. 60°
• C. 120°
• D. 330°

Answer: (D)

Identify what angle, $\theta$ , satisfies the following conditions.
$\tan\theta=-1$; $\cos\theta$ > $0$

• A. 45°
• B. 135°
• C. 315°
• D. 330°

Answer: (C)

Trig Values in Quadrants II, III, & IV Example 3

Understanding the unit circle is essential for mastering trigonometry, as it provides a visual representation of the relationships between angles and their corresponding sine, cosine, and tangent values. The unit circle is centered at the origin (0,0) with a radius of 1, and it is divided into four quadrants, each representing different angle measures in both degrees and radians.

To begin filling in the unit circle, start with the four quadrantal angles: 0 degrees (0 radians), 90 degrees (π/2 radians), 180 degrees (π radians), and 270 degrees (3π/2 radians). These angles correspond to the points (1,0), (0,1), (-1,0), and (0,-1) on the coordinate plane. The tangent values for these angles can be calculated as the ratio of the y-coordinate to the x-coordinate. For example, the tangent of 0 degrees is 0 (0/1), while the tangent of 90 degrees is undefined (1/0).

Next, focus on the common angles in the first quadrant: 30 degrees (π/6 radians), 45 degrees (π/4 radians), and 60 degrees (π/3 radians). These angles have reference angles that can help determine their measures in the other quadrants. For instance, in the second quadrant, the angle corresponding to a 30-degree reference angle is 150 degrees (180 - 30) or 5π/6 radians. In the third quadrant, it becomes 210 degrees (180 + 30) or 7π/6 radians, and in the fourth quadrant, it is 330 degrees (360 - 30) or 11π/6 radians.

When filling in the sine and cosine values for these angles, remember that in the first quadrant, all values are positive. The sine and cosine values for 30 degrees are 1/2 and √3/2, respectively. For 45 degrees, both sine and cosine are √2/2, and for 60 degrees, sine is √3/2 and cosine is 1/2. As you move to the other quadrants, the signs of these values change based on the quadrant's characteristics. In the second quadrant, sine remains positive while cosine is negative. In the third quadrant, both sine and cosine are negative, but tangent is positive. Finally, in the fourth quadrant, cosine is positive while sine is negative.

Utilizing the mnemonic "All Students Take Calculus" can help remember which trigonometric functions are positive in each quadrant: All (all functions positive in the first), Students (sine positive in the second), Take (tangent positive in the third), and Calculus (cosine positive in the fourth).

By practicing filling in the unit circle repeatedly, you will become more comfortable with the angles, their corresponding values, and the relationships between them. This foundational knowledge is crucial for solving more complex trigonometric problems and understanding periodic functions.

Coterminal Angles on the Unit Circle

Understanding coterminal angles is essential for evaluating trigonometric functions efficiently. Coterminal angles are angles that share the same terminal side when drawn in standard position. To find a coterminal angle, you can add or subtract multiples of \(360^\circ\) or \(2\pi\) radians. For example, to find the sine of \(390^\circ\), you can subtract \(360^\circ\) to arrive at \(30^\circ\). Since these angles are coterminal, their sine values are identical, making the sine of \(390^\circ\) equal to the sine of \(30^\circ\), which is \(\frac{1}{2}\).

Similarly, when evaluating the tangent of \(3\pi\), you can visualize this on the unit circle. A full rotation of \(2\pi\) plus an additional \(\pi\) brings you back to the angle \(\pi\). Thus, the tangent of \(3\pi\) is the same as the tangent of \(\pi\), which is \(0\).

For negative angles, such as \(-\frac{\pi}{4}\), the direction of measurement is clockwise. By moving clockwise from \(0\) to \(-\frac{\pi}{4}\), you can find the coterminal angle of \(\frac{7\pi}{4}\). The cosine of \(-\frac{\pi}{4}\) corresponds to the x-coordinate at \(\frac{7\pi}{4}\), which is \(\frac{\sqrt{2}}{2}\).

In summary, recognizing coterminal angles allows for quick identification of trigonometric values on the unit circle, simplifying calculations for both positive and negative angles. This understanding is crucial for mastering trigonometric functions and their applications.

For each expression, identify which coterminal angle to use & determine the exact value of the expression.
$\sin\frac{7\pi}{3}$

• A. $\frac12$
• B. $2$
• C. $\frac{\sqrt3}{2}$
• D. $\frac{2\sqrt3}{3}$

Answer: (C)

For each expression, identify which coterminal angle to use & determine the exact value of the expression.
$\tan765\degree$

• A. $-1$
• B. $1$
• C. $0$
• D. undefined

Answer: (B)

For each expression, identify which coterminal angle to use & determine the exact value of the expression.
$\cos\left(-\frac{10\pi}{4}\right)$

• A. $0$
• B. $1$
• C. $-1$
• D. $\frac{\sqrt2}{2}$

Answer: (A)

Secant, Cosecant, & Cotangent on the Unit Circle

In trigonometry, alongside the primary functions sine, cosine, and tangent, there are three important reciprocal functions: cosecant, secant, and cotangent. These functions are derived directly from the original trigonometric functions, allowing us to utilize the unit circle without needing additional information.

The cosecant function is defined as the reciprocal of sine, which can be expressed mathematically as:

$$ \text{csc}(\theta) = \frac{1}{\sin(\theta)} $$

On the unit circle, since sine corresponds to the y-coordinate, the cosecant can be calculated as:

$$ \text{csc}(\theta) = \frac{1}{y} $$

Similarly, the secant function is the reciprocal of cosine:

$$ \text{sec}(\theta) = \frac{1}{\cos(\theta)} $$

Here, cosine corresponds to the x-coordinate, so we find secant as:

$$ \text{sec}(\theta) = \frac{1}{x} $$

Lastly, the cotangent function is the reciprocal of tangent, which is defined as:

$$ \text{cot}(\theta) = \frac{1}{\tan(\theta)} $$

Since tangent is the ratio of sine to cosine (or y over x), cotangent can be expressed as:

$$ \text{cot}(\theta) = \frac{x}{y} $$

To illustrate these concepts, consider the following examples:

1. **Cosecant of \( \frac{\pi}{6} \)**: The sine of \( \frac{\pi}{6} \) is \( \frac{1}{2} \), so:

$$ \text{csc}\left(\frac{\pi}{6}\right) = \frac{1}{\frac{1}{2}} = 2 $$

2. **Cotangent of \( \frac{\pi}{4} \)**: At \( \frac{\pi}{4} \), both the x and y values are \( \frac{\sqrt{2}}{2} \), thus:

$$ \text{cot}\left(\frac{\pi}{4}\right) = \frac{\frac{\sqrt{2}}{2}}{\frac{\sqrt{2}}{2}} = 1 $$

3. **Secant of \( 0 \)**: The x value at \( 0 \) degrees is \( 1 \), leading to:

$$ \text{sec}(0) = \frac{1}{1} = 1 $$

Understanding these reciprocal functions enhances your ability to work with trigonometric identities and solve various problems involving angles and their relationships on the unit circle. Practice finding these values using the unit circle to solidify your understanding.

Evaluate each expression.
$\cot\left(\frac{11\pi}{6}\right)$

• A. $\frac12$
• B. $-\frac{\sqrt3}{3}$
• C. $-\sqrt3$
• D. $2$

Answer: (C)

Evaluate each expression.
$\csc225\degree$

• A. $1$
• B. $-\frac{\sqrt2}{2}$
• C. $\sqrt2$
• D. $-\sqrt2$

Answer: (D)

Evaluate each expression.
$\sec\left(\frac{\pi}{3}\right)$

• A. $\frac12$
• B. $2$
• C. $\frac{\sqrt3}{2}$
• D. $\frac{2\sqrt3}{2}$

Answer: (B)

Here’s what students ask on this topic:

What is the unit circle and why is it important in trigonometry?

The unit circle is a circle with a radius of 1, centered at the origin (0, 0) on a coordinate plane. It is crucial in trigonometry because it provides a geometric framework for understanding the relationships between angles and trigonometric functions. Each angle on the unit circle corresponds to a specific point (x, y), where x represents the cosine of the angle and y represents the sine. The unit circle also helps in defining trigonometric functions for all angles, including those greater than 90° or negative angles. Additionally, it simplifies calculations involving radians, reference angles, and periodicity of trig functions. The equation of the unit circle is:

$x^2+y^2=1$

.

How do you find the sine, cosine, and tangent of an angle using the unit circle?

To find the sine, cosine, and tangent of an angle using the unit circle, follow these steps:

1. Locate the angle on the unit circle. If the angle is in degrees or radians, find its corresponding point (x, y) on the circle.

2. The cosine of the angle is the x-coordinate of the point, and the sine is the y-coordinate.

3. To find the tangent, divide the sine (y) by the cosine (x):

$\tan \left(\theta \right)=\frac{y}{x}$

.

For example, at 45° (or π/4 radians), the point is (√2/2, √2/2). Thus, cos(45°) = √2/2, sin(45°) = √2/2, and tan(45°) = 1.

What are reference angles, and how are they used in the unit circle?

A reference angle is the acute angle formed between the terminal side of a given angle and the x-axis. It is always positive and lies between 0° and 90° (or 0 and π/2 radians). Reference angles are used to simplify the calculation of trigonometric values for angles outside the first quadrant by relating them to their corresponding first-quadrant angles.

To find a reference angle:

- For angles in Quadrant II, subtract the angle from 180° (or π).

- For angles in Quadrant III, subtract 180° (or π) from the angle.

- For angles in Quadrant IV, subtract the angle from 360° (or 2π).

For example, the reference angle for 150° is 30° because 180° - 150° = 30°. The trigonometric values of 150° are the same as those of 30°, but with appropriate signs based on the quadrant.

How do you determine the signs of trigonometric functions in different quadrants?

The signs of trigonometric functions depend on the quadrant in which the angle lies. Use the mnemonic "All Students Take Calculus" to remember:

- Quadrant I: All trigonometric functions (sine, cosine, tangent) are positive.

- Quadrant II: Only sine is positive; cosine and tangent are negative.

- Quadrant III: Only tangent is positive; sine and cosine are negative.

- Quadrant IV: Only cosine is positive; sine and tangent are negative.

This rule is based on the signs of the x and y coordinates of points on the unit circle. For example, in Quadrant II, x is negative, and y is positive, so cosine (x) is negative, sine (y) is positive, and tangent (y/x) is negative.

What are reciprocal trigonometric functions, and how are they calculated on the unit circle?

Reciprocal trigonometric functions are derived from the basic trig functions (sine, cosine, tangent) and are defined as follows:

- Cosecant (csc): Reciprocal of sine, csc(θ) = 1/sin(θ) = 1/y.

- Secant (sec): Reciprocal of cosine, sec(θ) = 1/cos(θ) = 1/x.

- Cotangent (cot): Reciprocal of tangent, cot(θ) = 1/tan(θ) = x/y.

To calculate these on the unit circle, locate the angle and its corresponding point (x, y). Use the x and y values to compute the reciprocal functions. For example, at 30° (or π/6 radians), the point is (√3/2, 1/2). Thus, csc(30°) = 2, sec(30°) = 2/√3, and cot(30°) = √3.