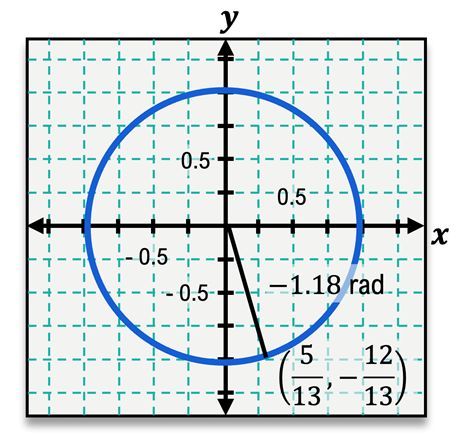
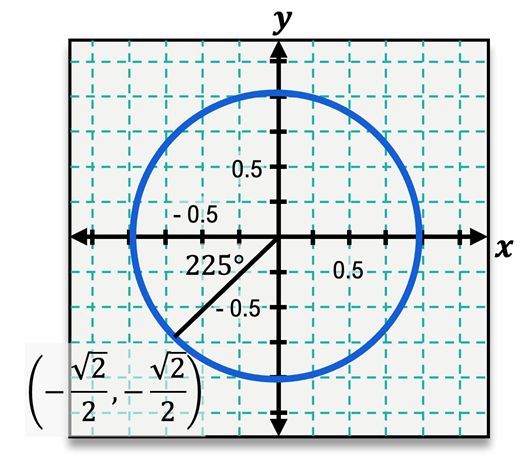
The unit circle is a fundamental concept in trigonometry, defined as a circle with a radius of one centered at the origin (0, 0) of a coordinate plane. It serves as a crucial tool for solving various trigonometric problems. The angles around the unit circle are measured in both degrees and radians, with a full rotation of 360 degrees corresponding to \(2\pi\) radians. The key angle measures include:
- 0 degrees (0 radians) at the point (1, 0)
- 90 degrees (\(\frac{\pi}{2}\) radians) at the point (0, 1)
- 180 degrees (\(\pi\) radians) at the point (-1, 0)
- 270 degrees (\(\frac{3\pi}{2}\) radians) at the point (0, -1)
- 360 degrees (\(2\pi\) radians) at the point (1, 0)
Each angle on the unit circle corresponds to specific coordinates (x, y) that can be derived from the circle's equation, which is given by:
\(x^2 + y^2 = 1\)
This equation indicates that any point (x, y) on the unit circle satisfies this relationship. To determine if a point lies on the unit circle, one can substitute the coordinates into the equation. For example, to check if the point (1, 1) is on the unit circle:
Substituting gives:
\(1^2 + 1^2 = 1 + 1 = 2\) (not equal to 1, so it is not on the unit circle).
In contrast, for the point \(\left(\frac{1}{2}, \frac{\sqrt{3}}{2}\right)\):
Substituting gives:
\(\left(\frac{1}{2}\right)^2 + \left(\frac{\sqrt{3}}{2}\right)^2 = \frac{1}{4} + \frac{3}{4} = 1\) (equal to 1, so it is on the unit circle).
Additionally, every point on the unit circle corresponds to a specific angle. For instance, the point \(\left(\frac{1}{2}, \frac{\sqrt{3}}{2}\right)\) corresponds to an angle of 60 degrees (or \(\frac{\pi}{3}\) radians). Understanding the unit circle and its properties is essential for mastering trigonometric functions and their applications.