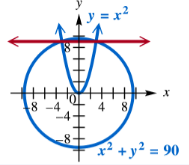
Answer each question. A line passes through the points of intersection of the graphs of y = x² and x² + y² = 90. What is the equation of this line?

Verified step by step guidance

1. Identify the points of intersection between the two graphs given by the equations \(y = \frac{3x^2}{50}\) and \(x^2 + y^2 = 136\). These points satisfy both equations simultaneously.
2. Substitute \(y = \frac{3x^2}{50}\) into the circle equation \(x^2 + y^2 = 136\) to get an equation in terms of \(x\) only: \(x^2 + \left(\frac{3x^2}{50}\right)^2 = 136\).
3. Simplify the equation to solve for \(x^2\): \(x^2 + \frac{9x^4}{2500} = 136\). Multiply through by 2500 to clear the denominator: \$2500x^2 + 9x^4 = 340000$.
4. Rearrange the equation into standard polynomial form: \$9x^4 + 2500x^2 - 340000 = 0\(. Solve this quadratic in terms of \)x^2\( to find the \)x$-coordinates of the intersection points.
5. Once the \(x\)-values are found, substitute back into \(y = \frac{3x^2}{50}\) to find the corresponding \(y\)-coordinates. Use these points to find the equation of the line passing through them by calculating the slope and using the point-slope form of a line.

Key Concepts

System of Equations and Intersection Points

To find the points where two graphs intersect, solve their equations simultaneously. This involves substituting one equation into the other or using algebraic methods to find common solutions (x, y) that satisfy both equations.

Equation of a Line Through Two Points

Once the intersection points are found, the equation of the line passing through these points can be determined using the slope formula (change in y over change in x) and the point-slope form of a line equation.

Substitution Method in Algebra

Substitution involves replacing one variable with an expression from another equation to reduce the system to a single equation. This method simplifies solving for one variable and is essential for finding intersection points in this problem.