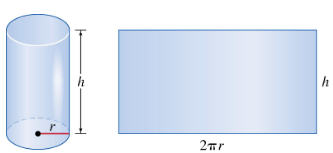
Solve each problem. Find the radius and height (to the nearest thousandth) of an open-ended cylinder with volume 50 in.³ and lateral surface area 65 in.².

Verified step by step guidance

1. Recall the formulas for the volume and lateral surface area of an open-ended cylinder. The volume \(V\) is given by \(V = \pi r^2 h\), where \(r\) is the radius and \(h\) is the height. The lateral surface area \(A\) (without the top and bottom) is \(A = 2 \pi r h\).
2. Write down the system of equations using the given values: \(\pi r^2 h = 50\) and \$2 \pi r h = 65$.
3. From the lateral surface area equation \$2 \pi r h = 65\(, solve for \)h\( in terms of \)r\(: \)h = \frac{65}{2 \pi r}$.
4. Substitute the expression for \(h\) into the volume equation: \(\pi r^2 \left( \frac{65}{2 \pi r} \right) = 50\). Simplify this equation to get an equation in terms of \(r\) only.
5. Solve the resulting equation for \(r\), then use the value of \(r\) to find \(h\) using the expression \(h = \frac{65}{2 \pi r}\). Round both \(r\) and \(h\) to the nearest thousandth.

Key Concepts

Volume of a Cylinder

The volume of a cylinder is calculated using the formula V = πr²h, where r is the radius and h is the height. This formula represents the amount of space inside the cylinder and is essential for relating the radius and height to the given volume.

Lateral Surface Area of an Open Cylinder

The lateral surface area of an open cylinder (without top and bottom) is given by A = 2πrh. This formula calculates the area of the curved surface, which helps establish a relationship between the radius and height based on the given surface area.

Solving Systems of Nonlinear Equations

Finding the radius and height requires solving two equations simultaneously: one for volume and one for lateral surface area. This involves techniques such as substitution or elimination to solve nonlinear equations involving π, r, and h.