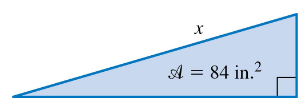
The following exercises are geometric in nature and lead to polynomial models. Solve each problem. A certain right triangle has area 84 in.². One leg of the triangle measures 1 in. less than the hypotenuse. Let x represent the length of the hypotenuse. Express the length of the leg mentioned above in terms of x. Give the domain of x.

Verified step by step guidance

1. Identify the variables: Let the hypotenuse be represented by \(x\). The leg mentioned is 1 inch less than the hypotenuse, so its length is \(x - 1\).
2. Since the triangle is right-angled, label the legs as \(a\) and \(b\), and the hypotenuse as \(c\). Here, one leg is \(x - 1\), and the hypotenuse is \(x\). We need to express the other leg in terms of \(x\) using the Pythagorean theorem.
3. Use the Pythagorean theorem: \(a^2 + b^2 = c^2\). Let the unknown leg be \(y\). Then, \((x - 1)^2 + y^2 = x^2\).
4. Express \(y^2\) in terms of \(x\): \(y^2 = x^2 - (x - 1)^2\). Simplify the right side to find \(y^2\) as a polynomial in \(x\).
5. Determine the domain of \(x\): Since \(x\) is the hypotenuse and must be longer than the leg \(x - 1\), and lengths must be positive, set \(x > 1\). Also, consider any restrictions from the area and the triangle inequality.

Key Concepts

Right Triangle Properties

A right triangle has one 90-degree angle, and its sides follow the Pythagorean theorem. The hypotenuse is the longest side opposite the right angle, and the legs are the two shorter sides. Understanding these relationships helps in expressing side lengths and solving for unknowns.

Algebraic Expression of Geometric Quantities

Translating geometric information into algebraic expressions involves defining variables and writing equations based on given relationships. Here, expressing one leg as 'x - 1' when x is the hypotenuse allows the problem to be modeled algebraically for further analysis.

Domain of a Variable in Context

The domain represents all possible values a variable can take based on the problem's constraints. For lengths, values must be positive and satisfy geometric conditions, such as the leg being shorter than the hypotenuse. Identifying the domain ensures solutions are realistic and meaningful.