Graph the rational function using transformations. f ( x ) = − 1 x + 3 f\left(x\right)=-\frac{1}{x}+3 f ( x ) = − x 1 + 3

Here, we're asked to graph the rational function using transformations. And here, I have the function g of x is equal to negative one over x plus 3, which I know I'm just going to be transforming the function 1 over x. So starting with step number 1 here, we want to go ahead and plot our vertical asymptote at x equals h. Now here, I don't have any horizontal shift, so h is simply 0. So my vertical asymptote goes right at that axis at x equals 0. Now, my horizontal axis or my horizontal asymptote will be at y equals to k. Here k is 3, so I need to go ahead and plot that horizontal asymptote right up here at y equals 3. Now for step 3, we want to determine if there is a reflection happening, which there is because I have this negative right outside here. So, yes, there is a reflection. I need to go ahead and reflect these points over the correct axis, in this case, the x axis, but it doesn't really matter because it's an odd function. It will end up being the same either way. So let's go ahead and reflect these two points here. Now, reflecting these points remember is the same as if I fold it at the axis and just kind of stamp those points on the other side. So here is the position of my new points. But now that I've reflected them, I also need to shift them according to what I have for h and k. And here h is 0 k is 3. So, I need to go ahead and shift these 3 units up. So shifting this first point I'm going to end up right here and then shifting my other point 3 units up I'm going to end up right here. So I have everything that I need for my new graph and I can go ahead and end up with my final step which is to sketch my curves approaching the asymptotes. So sketching my curves here, I know we're going to be approaching that horizontal asymptote here, the vertical asymptote here, and the same happening from this point. So we see we have the exact same shape, really similar looking function, it's just been formed from 1 over x. So let's go ahead and identify our domain and range. Now remember, our domain is always going to go from negative infinity until we reach that asymptote. So in this case it will be at 0 and then it will pick up on the other side continuing on from that asymptote to infinity, of course, enclosed in parentheses and not square brackets because those values are not included. Then the same thing for the range here from negative infinity to that asymptote, so in this case from negative infinity to 3, and then from 3 to infinity. So that's all for this problem we've completed our graph I'll see you in the next video.

5. Rational Functions

Graphing Rational Functions

College Algebra

5. Rational Functions

Graphing Rational Functions

Struggling with College Algebra?

Join thousands of students who trust us to help them ace their exams!

Multiple Choice

Graph the rational function using transformations.
$f$\left$(x$\right$)=-$\frac{1}{x}$+3$

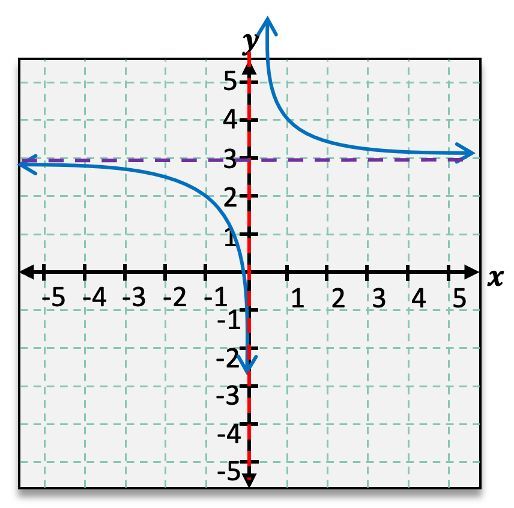
Graph of f(x) = -1/(x) + 3 showing vertical and horizontal asymptotes.

Graph of f(x) = -1/(x) + 3 with vertical and horizontal asymptotes.

Graph of f(x) = -1/(x) + 3 illustrating vertical and horizontal asymptotes.

Graph of f(x) = -1/(x) + 3 depicting vertical and horizontal asymptotes.

Verified step by step guidance

Start with the basic rational function f(x) = -1/x, which has a vertical asymptote at x = 0 and a horizontal asymptote at y = 0.

Identify the transformations applied to the function. The given function is f(x) = -1/x + 3, which indicates a vertical shift.

The '+3' in the function indicates a vertical shift upwards by 3 units. This means the horizontal asymptote will move from y = 0 to y = 3.

The vertical asymptote remains unchanged at x = 0 because there is no horizontal shift in the function.

Graph the transformed function by plotting the new asymptotes: a vertical asymptote at x = 0 and a horizontal asymptote at y = 3. Then, sketch the curve approaching these asymptotes, reflecting the original shape of the function f(x) = -1/x.

5:31m

Watch next

Master Graphing Rational Functions Using Transformations with a bite sized video explanation from Patrick

Graphing Rational Functions practice set

Problem sets built by lead tutors

Expert video explanations

Struggling with College Algebra?

Graph the rational function using transformations.f(x)=−1x+3f\(\left\)(x\(\right\))=-\(\frac{1}{x}\)+3f(x)=−x1+3

Watch next

Graphing Rational Functions practice set

Graph the rational function using transformations.
$f\(\left\)(x\(\right\))=-\(\frac{1}{x}\)+3$