Identify which graphs are not those of polynomial functions.

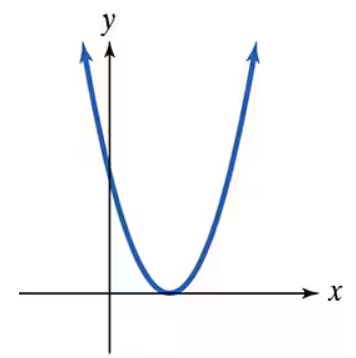
Verified step by step guidance

1. Step 1: Understand the characteristics of polynomial function graphs. Polynomial graphs are smooth and continuous curves without breaks, holes, or sharp corners.
2. Step 2: Observe the given graph carefully. Notice that the curve is smooth and continuous, with no breaks or sharp turns.
3. Step 3: Identify the general shape of the graph. The graph appears to be a parabola opening downward, which is typical of a quadratic polynomial function of the form \(y = ax^2 + bx + c\) where \(a < 0\).
4. Step 4: Confirm that the graph does not have any features that contradict polynomial behavior, such as vertical asymptotes or discontinuities.
5. Step 5: Conclude that since the graph is smooth, continuous, and resembles a parabola, it is consistent with the graph of a polynomial function.

Key Concepts

Polynomial Functions

Polynomial functions are algebraic expressions involving variables raised to non-negative integer powers, combined using addition, subtraction, and multiplication. Their graphs are smooth, continuous curves without breaks or sharp corners, and they extend infinitely in both directions.

Graph Characteristics of Polynomial Functions

Graphs of polynomial functions are continuous and smooth, with no gaps or cusps. They can have turning points, but the number of turning points is limited by the degree of the polynomial. The end behavior of the graph depends on the leading term's degree and coefficient.

Identifying Non-Polynomial Graphs

Graphs that are not polynomial functions often have discontinuities, sharp corners, vertical asymptotes, or oscillations that do not smooth out. Recognizing these features helps distinguish polynomial graphs from others like rational, exponential, or piecewise functions.