Back
BackProblem 11
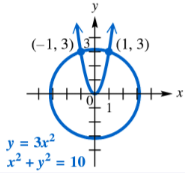
Verify that the points of intersection specified on the graph of each nonlinear system are solutions of the system by substituting directly into both equations.
y = 3x2
x2 + y2 = 10
Problem 15
Solve each nonlinear system of equations. Give all solutions, including those with nonreal complex components.
x2 - y = 0
x + y = 2
Problem 17
Solve each nonlinear system of equations. Give all solutions, including those with nonreal complex components.
y = x2 - 2x + 1
x - 3y = -1
Problem 37
Solve each nonlinear system of equations. Give all solutions, including those with nonreal complex components.
2xy + 1 = 0
x + 16y = 2
Problem 39
Solve each nonlinear system of equations. Give all solutions, including those with nonreal complex components.
3x2 - y2 = 11
xy = 12
Problem 55
Solve each problem using a system of equations in two variables. See Example 6. Find two numbers whose sum is 17 and whose product is 42.
Problem 57
Solve each problem using a system of equations in two variables. See Example 6. Find two numbers whose squares have a sum of 100 and a difference of 28.
Problem 59
Solve each problem using a system of equations in two variables. See Example 6. Find two numbers whose ratio is 9 to 2 and whose product is 162.
Problem 61
Solve each problem using a system of equations in two variables. See Example 6. The longest side of a right triangle is 13 m in length. One of the other sides is 7 m longer than the shortest side. Find the lengths of the two shorter sides of the triangle.
Problem 63
Answer each question. Does the straight line 3x - 2y = 9 intersect the circle x2 + y2 = 25? (Hint: To find out, solve the system formed by these two equations.)
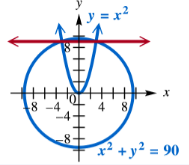
Problem 65
Answer each question. A line passes through the points of intersection of the graphs of y = x2 and x2 + y2 = 90. What is the equation of this line?
Problem 75
Consider the following nonlinear system. Work Exercises 75 –80 in order.
y = | x - 1 |
y = x2 - 4
How is the graph of y = | x - 1 | obtained by transforming the graph of y = | x |?
Problem 77
Consider the following nonlinear system. Work Exercises 75 –80 in order.
y = | x - 1 |
y = x2 - 4
Use the definition of absolute value to write y = | x - 1 | as a piecewise-defined function.
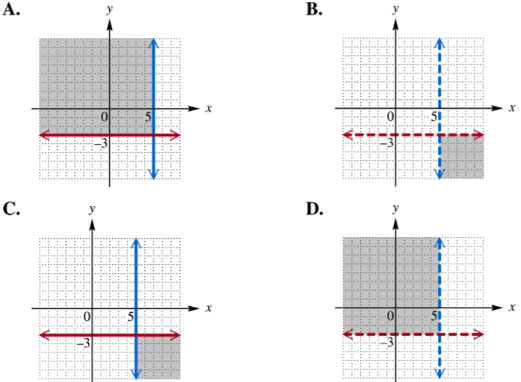
Problem 1
Match each system of inequalities with the correct graph from choices A–D. x ≥ 5 y ≤ -3
Problem 11
Graph each inequality. x + 2y ≤ 6
Problem 19
Graph each inequality. x ≤ 3
Problem 21
Graph each inequality. y < 3x2 + 2
Problem 23
Graph each inequality. y > (x - 1)2 + 2
Problem 25
Graph each inequality. x2 + (y + 3)2 ≤ 16
Problem 27
Graph each inequality. y > 2x + 1
Problem 28
Graph each inequality. y ≤ log(x - 1) - 2
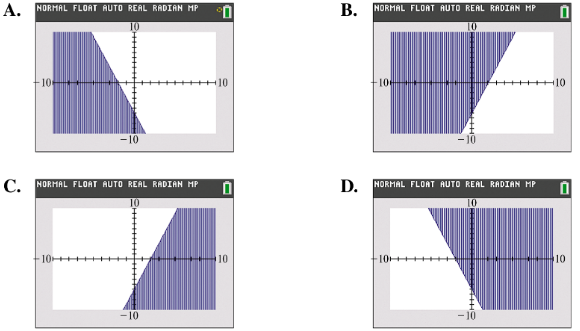
Problem 35
Match each inequality with the appropriate calculator graph in A–D. Do not use a calculator y ≤ -3x - 6
Problem 37
Graph the solution set of each system of inequalities.
x + y ≥ 0
2x - y ≥ 3
Problem 39
Graph the solution set of each system of inequalities.
2x + y > 2
x - 3y < 6
Problem 41
Graph the solution set of each system of inequalities.
3x + 5y ≤ 15
x2 + y2 < 9
Problem 43
Graph the solution set of each system of inequalities.
4x - 3y ≤ 12
y ≤ x2
Problem 48
Graph the solution set of each system of inequalities.
y ≥ (x - 2)2 + 3
y ≤ -(x - 1)2 + 6
Problem 51
Graph the solution set of each system of inequalities.
y ≥ x2 + 4x + 4
y < -x2
Problem 53
Graph the solution set of each system of inequalities.
Problem 57
Graph the solution set of each system of inequalities.