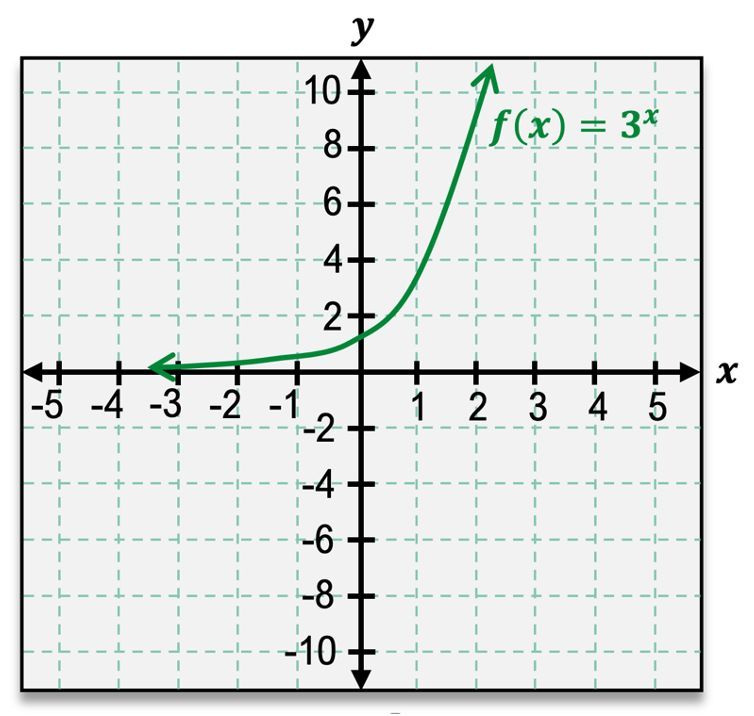
Graphing exponential functions, such as \( f(x) = 2^x \), is a straightforward process compared to polynomial and rational functions. To begin, we can generate ordered pairs by substituting values for \( x \). For instance, when \( x = 0 \), \( f(0) = 2^0 = 1 \). This gives us our first point at (0, 1). Continuing with \( x = 1 \), we find \( f(1) = 2^1 = 2 \), leading to the point (1, 2). As \( x \) increases, the function grows rapidly: \( f(2) = 4 \) and \( f(3) = 8 \). For larger values, such as \( x = 10 \), \( f(10) = 2^{10} = 1024 \). This indicates that as \( x \) approaches infinity, \( f(x) \) also approaches infinity, demonstrating the end behavior of the graph.
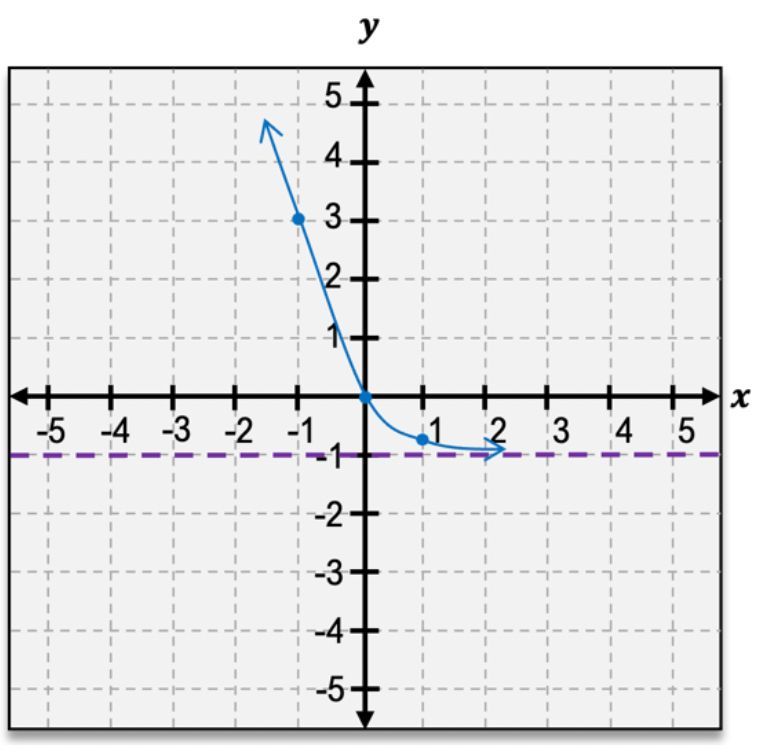
When considering negative values of \( x \), for example, \( x = -1 \), we calculate \( f(-1) = 2^{-1} = \frac{1}{2} \), resulting in the point (-1, 0.5). As \( x \) becomes more negative, the function values decrease, approaching 0 but never actually reaching it. This behavior indicates the presence of a horizontal asymptote at \( y = 0 \), which can be represented by a dashed line on the graph.
Exponential functions are continuous, meaning there are no breaks in the graph. Additionally, they exhibit a one-to-one property, where each \( x \) value corresponds to a unique \( y \) value, allowing the graph to pass the horizontal line test. The overall shape of the graph resembles a stretched lowercase 'e', which can help in visualizing its form.
The domain of any exponential function is all real numbers, expressed as \( (-\infty, \infty) \). The range, however, is determined by the asymptote; for \( f(x) = 2^x \), the range is \( (0, \infty) \), indicating that \( y \) values are always positive and never include 0.
When exploring other exponential functions of the form \( f(x) = b^x \), the base \( b \) significantly influences the graph's behavior. If \( b > 1 \), the graph will increase, while if \( 0 < b < 1 \), the graph will decrease. The steepness of the graph also varies with the base: for bases greater than 1, larger values of \( b \) yield steeper graphs, whereas for bases between 0 and 1, smaller values of \( b \) result in steeper declines.
Understanding these characteristics of exponential functions equips you with the tools to graph and analyze them effectively. Practice with different bases will further solidify your comprehension of their unique properties.