Titrations play a crucial role in stoichiometric reactions and are a recurring theme in analytical chemistry. Understanding the concept of gravimetric analysis is essential, as it helps determine the amount of product that can be isolated from a chemical reaction. The calculations involved in this process are referred to as stoichiometry, which utilizes a stoichiometric chart derived from a balanced chemical equation.
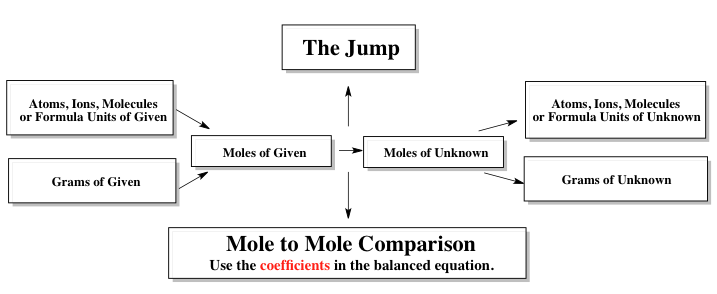
The stoichiometric chart serves as a tool to relate known quantities of reactants or products to unknown quantities within a balanced equation. Typically, the given information may be presented in various units such as grams or moles. To convert grams to moles, the molecular weight of the compound is used. When dealing with atoms, ions, molecules, or formula units, Avogadro's number, \(6.022 \times 10^{23}\), is applied to transition to moles. It is important to note the distinctions between these terms: "atoms" refers to neutral single elements (e.g., O for oxygen), "ions" denotes charged single elements, "molecules" pertains to covalent compounds (nonmetals), and "formula units" describes ionic compounds (combinations of positive and negative ions).
In practice, the stoichiometric chart allows us to navigate from known values to unknown quantities, which may be expressed in moles, atoms, ions, molecules, formula units, or grams. This transition is often referred to as making a "jump" from the known to the unknown. To facilitate this leap, a mole-to-mole comparison is essential, relying on the coefficients from the balanced equation. This foundational understanding of the stoichiometric chart is vital for performing titrations and other stoichiometric calculations effectively.