Entropy is a fundamental concept in thermodynamics, closely linked to the second law, which states that molecular systems naturally progress towards a state of maximum disorder or randomness. This principle implies that the total entropy of the universe is always increasing, indicating a trend towards chaos and degradation. As galaxies evolve, stars may explode into supernovas, ultimately leading to black holes, illustrating the universe's tendency towards disorder.
The change in entropy, denoted as ΔS, can be expressed mathematically as:
ΔSuniverse = ΔSsystem + ΔSsurroundings
This equation emphasizes that the total change in entropy is always greater than zero, reflecting the second law of thermodynamics.
Entropy can also be analyzed in terms of phase changes. For instance, when a substance transitions from solid to liquid (melting or fusion) or from liquid to gas (vaporization), the distance between molecules increases, leading to greater disorder. Consequently, these processes result in a positive change in entropy (ΔS > 0). Conversely, when a substance transitions from gas to liquid to solid, the molecules become more ordered, resulting in a decrease in entropy (ΔS < 0).
It is important to note that while entropy typically increases, it can theoretically reach zero at absolute zero temperature (0 Kelvin), as stated in the third law of thermodynamics. At this temperature, all molecular motion ceases, and the entropy of a substance is exactly zero. However, achieving 0 Kelvin is highly theoretical, as the average temperature of the universe is approximately 2 Kelvin.
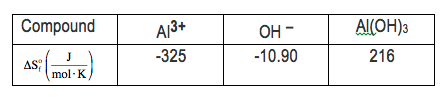
Understanding these principles of entropy lays the groundwork for comparing the entropies of different compounds, which will be explored further in subsequent discussions.